2017年浙江省温州市中考数学试卷

试卷更新日期：2017-07-24 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣6的相反数是（）

A、6 B、1 C、0 D、﹣6

查看试题解析
2.
某校学生到校方式情况的统计图如图所示，若该校步行到校的学生有100人，则乘公共汽车到校的学生有（）

A、75人 B、100人 C、125人 D、200人

查看试题解析
3.
某运动会颁奖台如图所示，它的主视图是（）

A、 B、 C、 D、

查看试题解析
4. 下列选项中的整数，与 $\sqrt{17}$ 最接近的是（）

A、3 B、4 C、5 D、6

查看试题解析
5. 温州某企业车间有50名工人，某一天他们生产的机器零件个数统计如下表：
零件个数（个）
5
6
7
8
人数（人）
3
15
22
10
表中表示零件个数的数据中，众数是（）

A、5个 B、6个 C、7个 D、8个

查看试题解析
6. 已知点（﹣1，y₁），（4，y₂）在一次函数y=3x﹣2的图象上，则y₁ ， y₂ ， 0的大小关系是（）

A、0＜y₁＜y₂ B、y₁＜0＜y₂ C、y₁＜y₂＜0 D、y₂＜0＜y₁

查看试题解析
7.
如图，一辆小车沿倾斜角为α的斜坡向上行驶13米，已知cosα= $\frac{12}{13}$ ，则小车上升的高度是（）

A、5米 B、6米 C、6.5米 D、12米

查看试题解析
8. 我们知道方程x²+2x﹣3=0的解是x₁=1，x₂=﹣3，现给出另一个方程（2x+3）²+2（2x+3）﹣3=0，它的解是（）

A、x₁=1，x₂=3 B、x₁=1，x₂=﹣3 C、x₁=﹣1，x₂=3 D、x₁=﹣1，x₂=﹣3

查看试题解析
9.
四个全等的直角三角形按图示方式围成正方形ABCD，过各较长直角边的中点作垂线，围成面积为S的小正方形EFGH．已知AM为Rt△ABM较长直角边，AM=2 $\sqrt{2}$ EF，则正方形ABCD的面积为（）

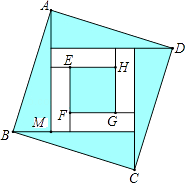A、12S B、10S C、9S D、8S

查看试题解析
10.
我们把1，1，2，3，5，8，13，21，…这组数称为斐波那契数列，为了进一步研究，依次以这列数为半径作90°圆弧 $\hat{P_{1} P_{2}}$ ， $\hat{P_{2} P_{3}}$ ， $\hat{P_{3} P_{4}}$ ，…得到斐波那契螺旋线，然后顺次连结P₁P₂ ， P₂P₃ ， P₃P₄ ， …得到螺旋折线（如图），已知点P₁（0，1），P₂（﹣1，0），P₃（0，﹣1），则该折线上的点P₉的坐标为（）

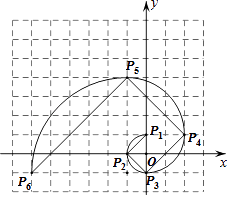A、（﹣6，24） B、（﹣6，25） C、（﹣5，24） D、（﹣5，25）

查看试题解析

二、填空题

11. 分解因式：m²+4m= ．

查看试题解析
12. 数据1，3，5，12，a，其中整数a是这组数据的中位数，则该组数据的平均数是．

查看试题解析
13. 已知扇形的面积为3π，圆心角为120°，则它的半径为．

查看试题解析
14. 甲、乙工程队分别承接了160米、200米的管道铺设任务，已知乙比甲每天多铺设5米，甲、乙完成铺设任务的时间相同，问甲每天铺设多少米？设甲每天铺设x米，根据题意可列出方程：．

查看试题解析
15.
如图，矩形OABC的边OA，OC分别在x轴、y轴上，点B在第一象限，点D在边BC上，且∠AOD=30°，四边形OA′B′D与四边形OABD关于直线OD对称（点A′和A，B′和B分别对应）．若AB=1，反比例函数y= $\frac{k}{x}$ （k≠0）的图象恰好经过点A′，B，则k的值为．

查看试题解析
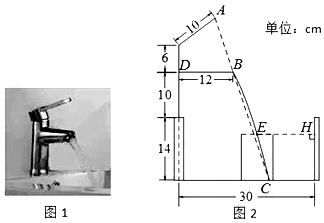
16.
小明家的洗手盆上装有一种抬启式水龙头（如图1），完全开启后，水流路线呈抛物线，把手端点A，出水口B和落水点C恰好在同一直线上，点A至出水管BD的距离为12cm，洗手盆及水龙头的相关数据如图2所示，现用高10.2cm的圆柱型水杯去接水，若水流所在抛物线经过点D和杯子上底面中心E，则点E到洗手盆内侧的距离EH为cm．

查看试题解析

三、解答题

17. 计算题

(1)、计算：2×（﹣3）+（﹣1）²+ $\sqrt{8}$ ；

(2)、化简：（1+a）（1﹣a）+a（a﹣2）．

查看试题解析
18.
如图，在五边形ABCDE中，∠BCD=∠EDC=90°，BC=ED，AC=AD．

(1)、求证：△ABC≌△AED；

(2)、当∠B=140°时，求∠BAE的度数．

查看试题解析
19.
为培养学生数学学习兴趣，某校七年级准备开设“神奇魔方”、“魅力数独”、“数学故事”、“趣题巧解”四门选修课（每位学生必须且只选其中一门）．

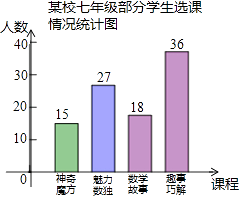(1)、学校对七年级部分学生进行选课调查，得到如图所示的统计图．根据该统计图，请估计该校七年级480名学生选“数学故事”的人数．

(2)、学校将选“数学故事”的学生分成人数相等的A，B，C三个班，小聪、小慧都选择了“数学故事”，已知小聪不在A班，求他和小慧被分到同一个班的概率．（要求列表或画树状图）

查看试题解析
20. 在直角坐标系中，我们把横、纵坐标都为整数的点称为整点，记顶点都是整点的三角形为整点三角形．如图，已知整点A（2，3），B（4，4），请在所给网格区域（含边界）上按要求画整点三角形．

(1)、
在图1中画一个△PAB，使点P的横、纵坐标之和等于点A的横坐标；

(2)、
在图2中画一个△PAB，使点P，B横坐标的平方和等于它们纵坐标和的4倍．

查看试题解析
21.
如图，在△ABC中，AC=BC，∠ACB=90°，⊙O（圆心O在△ABC内部）经过B、C两点，交AB于点E，过点E作⊙O的切线交AC于点F．延长CO交AB于点G，作ED∥AC交CG于点D

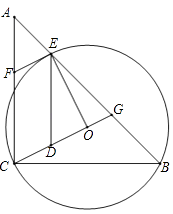(1)、求证：四边形CDEF是平行四边形；

(2)、若BC=3，tan∠DEF=2，求BG的值．

查看试题解析
22.
如图，过抛物线y= $\frac{1}{4}$ x²﹣2x上一点A作x轴的平行线，交抛物线于另一点B，交y轴于点C，已知点A的横坐标为﹣2．

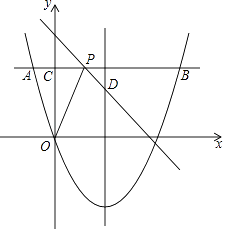(1)、求抛物线的对称轴和点B的坐标；

(2)、在AB上任取一点P，连结OP，作点C关于直线OP的对称点D；
①连结BD，求BD的最小值；
②当点D落在抛物线的对称轴上，且在x轴上方时，求直线PD的函数表达式．

查看试题解析
23.
小黄准备给长8m，宽6m的长方形客厅铺设瓷砖，现将其划分成一个长方形ABCD区域Ⅰ（阴影部分）和一个环形区域Ⅱ（空白部分），其中区域Ⅰ用甲、乙、丙三种瓷砖铺设，且满足PQ∥AD，如图所示．

(1)、若区域Ⅰ的三种瓷砖均价为300元/m² ，面积为S（m²），区域Ⅱ的瓷砖均价为200元/m² ，且两区域的瓷砖总价为不超过12000元，求S的最大值；

(2)、若区域Ⅰ满足AB：BC=2：3，区域Ⅱ四周宽度相等
①求AB，BC的长；
②若甲、丙两瓷砖单价之和为300元/m² ，乙、丙瓷砖单价之比为5：3，且区域Ⅰ的三种瓷砖总价为4800元，求丙瓷砖单价的取值范围．

查看试题解析
24.
如图，已知线段AB=2，MN⊥AB于点M，且AM=BM，P是射线MN上一动点，E，D分别是PA，PB的中点，过点A，M，D的圆与BP的另一交点C（点C在线段BD上），连结AC，DE．

(1)、当∠APB=28°时，求∠B和 $\hat{C M}$ 的度数；

(2)、求证：AC=AB．

(3)、在点P的运动过程中
①当MP=4时，取四边形ACDE一边的两端点和线段MP上一点Q，若以这三点为顶点的三角形是直角三角形，且Q为锐角顶点，求所有满足条件的MQ的值；
②记AP与圆的另一个交点为F，将点F绕点D旋转90°得到点G，当点G恰好落在MN上时，连结AG，CG，DG，EG，直接写出△ACG和△DEG的面积之比．

查看试题解析

零件个数（个）	5	6	7	8
人数（人）	3	15	22	10