2017年山西省中考数学试卷
试卷更新日期:2017-07-24 类型:中考真卷
一、选择题
-
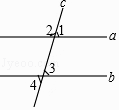
1. 计算﹣1+2的结果是( )A、﹣3 B、﹣1 C、1 D、32. 如图,直线a,b被直线c所截,下列条件不能判定直线a与b平行的是( )
 A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠43. 在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同.若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( )A、众数 B、平均数 C、中位数 D、方差4. 将不等式组 的解集表示在数轴上,下面表示正确的是( )A、
A、∠1=∠3 B、∠2+∠4=180° C、∠1=∠4 D、∠3=∠43. 在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同.若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( )A、众数 B、平均数 C、中位数 D、方差4. 将不等式组 的解集表示在数轴上,下面表示正确的是( )A、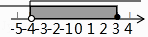 B、
B、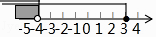 C、
C、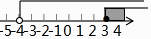 D、
D、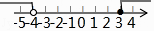 5. 下列运算错误的是( )A、( ﹣1)0=1 B、(﹣3)2÷ = C、5x2﹣6x2=﹣x2 D、(2m3)2÷(2m)2=m46. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )
5. 下列运算错误的是( )A、( ﹣1)0=1 B、(﹣3)2÷ = C、5x2﹣6x2=﹣x2 D、(2m3)2÷(2m)2=m46. 如图,将矩形纸片ABCD沿BD折叠,得到△BC′D,C′D与AB交于点E.若∠1=35°,则∠2的度数为( )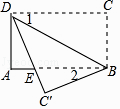 A、20° B、30° C、35° D、55°7. 化简 ﹣ 的结果是( )A、﹣x2+2x B、﹣x2+6x C、﹣ D、8. 2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计,仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为( )
A、20° B、30° C、35° D、55°7. 化简 ﹣ 的结果是( )A、﹣x2+2x B、﹣x2+6x C、﹣ D、8. 2017年5月18日,我国宣布在南海神狐海域成功试采可燃冰,成为世界上首个在海域连续稳定产气的国家.据粗略估计,仅南海北部陆坡的可燃冰资源就达到186亿吨油当量,达到我国陆上石油资源总量的50%.数据186亿吨用科学记数法可表示为( ) A、186×108吨 B、18.6×109吨 C、1.86×1010吨 D、0.186×1011吨9. 公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ,导致了第一次数学危机, 是无理数的证明如下:
A、186×108吨 B、18.6×109吨 C、1.86×1010吨 D、0.186×1011吨9. 公元前5世纪,毕达哥拉斯学派中的一名成员希伯索斯发现了无理数 ,导致了第一次数学危机, 是无理数的证明如下:假设 是有理数,那么它可以表示成 (p与q是互质的两个正整数).于是( )2=( )2=2,所以,q2=2p2 . 于是q2是偶数,进而q是偶数,从而可设q=2m,所以(2m)2=2p2 , p2=2m2 , 于是可得p也是偶数.这与“p与q是互质的两个正整数”矛盾.从而可知“ 是有理数”的假设不成立,所以, 是无理数.
这种证明“ 是无理数”的方法是( )
A、综合法 B、反证法 C、举反例法 D、数学归纳法10. 如图是某商品的标志图案,AC与BD是⊙O的两条直径,首尾顺次连接点A,B,C,D,得到四边形ABCD.若AC=10cm,∠BAC=36°,则图中阴影部分的面积为( )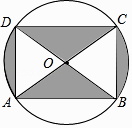 A、5πcm2 B、10πcm2 C、15πcm2 D、20πcm2
A、5πcm2 B、10πcm2 C、15πcm2 D、20πcm2二、填空题
-
11. 计算:4 ﹣9 = .12. 某商店经销一种品牌的洗衣机,其中某一型号的洗衣机每台进价为a元,商店将进价提高20%后作为零售价进行销售,一段时间后,商店又以9折优惠价促销,这时该型号洗衣机的零售价为元.
 13.
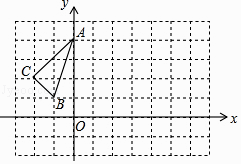
13.如图,已知△ABC三个顶点的坐标分别为A(0,4),B(﹣1,1),C(﹣2,2),将△ABC向右平移4个单位,得到△A′B′C′,点A,B,C的对应点分别为A′、B′、C′,再将△A′B′C′绕点B′顺时针旋转90°,得到△A″B″C″,点A′、B′、C′的对应点分别为A″、B″、C″,则点A″的坐标为 .
 14.
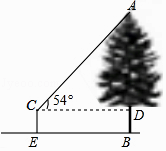
14.如图,创新小组要测量公园内一棵树的高度AB,其中一名小组成员站在距离树10米的点E处,测得树顶A的仰角为54°.已知测角仪的架高CE=1.5米,则这棵树的高度为米.(结果保留一位小数.参考数据:sin54°=0.8090,cos54°=0.5878,tan54°=1.3764)
 15. 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为 cm.
15. 一副三角板按如图方式摆放,得到△ABD和△BCD,其中∠ADB=∠BCD=90°,∠A=60°,∠CBD=45°,E为AB的中点,过点E作EF⊥CD于点F.若AD=4cm,则EF的长为 cm.
三、解答题
-
16. 计算题(1)、计算:(﹣2)3+( )﹣2﹣ •sin45°
(2)、分解因式:(y+2x)2﹣(x+2y)2 .
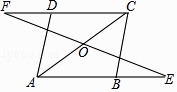
17. 已知:如图,在▱ABCD中,延长AB至点E,延长CD至点F,使得BE=DF.连接EF,与对角线AC交于点O.求证:OE=OF.
 18. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y= (k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.
18. 如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,其边长为2,点A,点C分别在x轴,y轴的正半轴上,函数y=2x的图象与CB交于点D,函数y= (k为常数,k≠0)的图象经过点D,与AB交于点E,与函数y=2x的图象在第三象限内交于点F,连接AF、EF.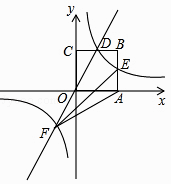 (1)、求函数y= 的表达式,并直接写出E、F两点的坐标;(2)、求△AEF的面积.19. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题:
(1)、求函数y= 的表达式,并直接写出E、F两点的坐标;(2)、求△AEF的面积.19. “春种一粒粟,秋收万颗子”,唐代诗人李绅这句诗中的“粟”即谷子(去皮后则称为“小米”),被誉为中华民族的哺育作物.我省有着“小杂粮王国”的美誉,谷子作为我省杂粮谷物中的大类,其种植面积已连续三年全国第一.2016年全国谷子种植面积为2000万亩,年总产量为150万吨,我省谷子平均亩产量为160kg,国内其他地区谷子的平均亩产量为60kg,请解答下列问题: (1)、求我省2016年谷子的种植面积是多少万亩.(2)、2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子?20.
(1)、求我省2016年谷子的种植面积是多少万亩.(2)、2017年,若我省谷子的平均亩产量仍保持160kg不变,要使我省谷子的年总产量不低于52万吨,那么,今年我省至少应再多种植多少万亩的谷子?20.从共享单车,共享汽车等共享出行到共享充电宝,共享雨伞等共享物品,各式各样的共享经济模式在各个领域迅速普及应用,越来越多的企业与个人成为参与者与受益者.根据国家信息中心发布的《中国分享经济发展报告2017》显示,2016年我国共享经济市场交易额约为34520亿元,比上年增长103%;超6亿人参与共享经济活动,比上年增加约1亿人.
如图是源于该报告中的中国共享经济重点领域市场规模统计图:
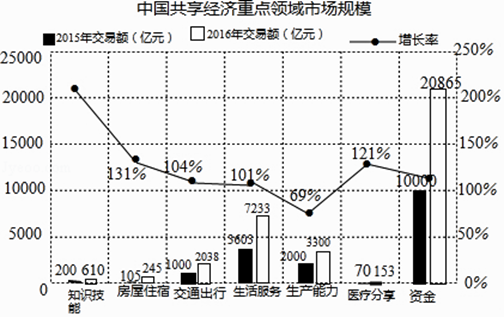 (1)、请根据统计图解答下列问题:
(1)、请根据统计图解答下列问题:①图中涉及的七个重点领域中,2016年交易额的中位数是亿元.
②请分别计算图中的“知识技能”和“资金”两个重点领域从2015年到2016年交易额的增长率(精确到1%),并就这两个重点领域中的一个分别从交易额和增长率两个方面,谈谈你的认识.
(2)、小宇和小强分别对共享经济中的“共享出行”和“共享知识”最感兴趣,他们上网查阅了相关资料,顺便收集到四个共享经济领域的图标,并将其制成编号为A,B,C,D的四张卡片(除编号和内容外,其余完全相同)他们将这四张卡片背面朝上,洗匀放好,从中随机抽取一张(不放回),再从中随机抽取一张,请用列表或画树状图的方法求抽到的两张卡片恰好是“共享出行”和“共享知识”的概率(这四张卡片分别用它们的编号A,B,C,D表示)
 21. 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.
21. 如图,△ABC内接于⊙O,且AB为⊙O的直径,OD⊥AB,与AC交于点E,与过点C的⊙O的切线交于点D.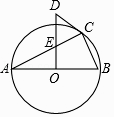 (1)、若AC=4,BC=2,求OE的长.(2)、试判断∠A与∠CDE的数量关系,并说明理由.22.
(1)、若AC=4,BC=2,求OE的长.(2)、试判断∠A与∠CDE的数量关系,并说明理由.22.综合与实践
背景阅读 早在三千多年前,我国周朝数学家商高就提出:将一根直尺折成一个直角,如果勾等于三,股等于四,那么弦就等于五,即“勾三、股四、弦五”.它被记载于我国古代著名数学著作《周髀算经》中,为了方便,在本题中,我们把三边的比为3:4:5的三角形称为(3,4,5)型三角形,例如:三边长分别为9,12,15或3 ,4 ,5 的三角形就是(3,4,5)型三角形,用矩形纸片按下面的操作方法可以折出这种类型的三角形.
实践操作 如图1,在矩形纸片ABCD中,AD=8cm,AB=12cm.
第一步:如图2,将图1中的矩形纸片ABCD沿过点A的直线折叠,使点D落在AB上的点E处,折痕为AF,再沿EF折叠,然后把纸片展平.
第二步:如图3,将图2中的矩形纸片再次折叠,使点D与点F重合,折痕为GH,然后展平,隐去AF.
第三步:如图4,将图3中的矩形纸片沿AH折叠,得到△AD′H,再沿AD′折叠,折痕为AM,AM与折痕EF交于点N,然后展平.
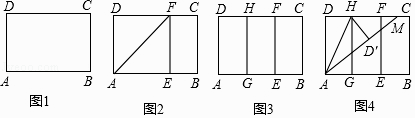 (1)、请在图2中证明四边形AEFD是正方形.(2)、请在图4中判断NF与ND′的数量关系,并加以证明;(3)、请在图4中证明△AEN(3,4,5)型三角形;(4)、在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.23.
(1)、请在图2中证明四边形AEFD是正方形.(2)、请在图4中判断NF与ND′的数量关系,并加以证明;(3)、请在图4中证明△AEN(3,4,5)型三角形;(4)、在不添加字母的情况下,图4中还有哪些三角形是(3,4,5)型三角形?请找出并直接写出它们的名称.23.如图,抛物线y=﹣ x2+ x+3 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,连接AC、BC.点P沿AC以每秒1个单位长度的速度由点A向点C运动,同时,点Q沿BO以每秒2个单位长度的速度由点B向点O运动,当一个点停止运动时,另一个点也随之停止运动,连接PQ.过点Q作QD⊥x轴,与抛物线交于点D,与BC交于点E,连接PD,与BC交于点F.设点P的运动时间为t秒(t>0).
 (1)、求直线BC的函数表达式;(2)、①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)
(1)、求直线BC的函数表达式;(2)、①直接写出P,D两点的坐标(用含t的代数式表示,结果需化简)②在点P、Q运动的过程中,当PQ=PD时,求t的值;
(3)、试探究在点P,Q运动的过程中,是否存在某一时刻,使得点F为PD的中点?若存在,请直接写出此时t的值与点F的坐标;若不存在,请说明理由.