2017年内蒙古包头市中考数学试卷
试卷更新日期:2017-07-24 类型:中考真卷
一、选择题
-
1. 计算( )﹣1所得结果是( )A、﹣2 B、 C、 D、22. a2=1,b是2的相反数,则a+b的值为( )A、﹣3 B、﹣1 C、﹣1或﹣3 D、1或﹣33. 一组数据5,7,8,10,12,12,44的众数是( )A、10 B、12 C、14 D、444. 将一个无盖正方体形状盒子的表面沿某些棱剪开,展开后不能得到的平面图形是( )A、
 B、
B、 C、
C、 D、
D、 5. 下列说法中正确的是( )A、8的立方根是±2 B、 是一个最简二次根式 C、函数y= 的自变量x的取值范围是x>1 D、在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称6. 若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )A、2cm B、4cm C、6cm D、8cm7. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外部相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为( )A、 B、 C、 D、8. 若关于x的不等式x﹣ <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定9. 如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ,则图中阴影部分的面积为( )
5. 下列说法中正确的是( )A、8的立方根是±2 B、 是一个最简二次根式 C、函数y= 的自变量x的取值范围是x>1 D、在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称6. 若等腰三角形的周长为10cm,其中一边长为2cm,则该等腰三角形的底边长为( )A、2cm B、4cm C、6cm D、8cm7. 在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外部相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为 ,则随机摸出一个红球的概率为( )A、 B、 C、 D、8. 若关于x的不等式x﹣ <1的解集为x<1,则关于x的一元二次方程x2+ax+1=0根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、无法确定9. 如图,在△ABC中,AB=AC,∠ABC=45°,以AB为直径的⊙O交BC于点D,若BC=4 ,则图中阴影部分的面积为( ) A、π+1 B、π+2 C、2π+2 D、4π+110. 已知下列命题:
A、π+1 B、π+2 C、2π+2 D、4π+110. 已知下列命题:①若 >1,则a>b;
②若a+b=0,则|a|=|b|;
③等边三角形的三个内角都相等;
④底角相等的两个等腰三角形全等.
其中原命题与逆命题均为真命题的个数是( )
A、1个 B、2个 C、3个 D、4个11. 已知一次函数y1=4x,二次函数y2=2x2+2,在实数范围内,对于x的同一个值,这两个函数所对应的函数值为y1与y2 , 则下列关系正确的是( )A、y1>y2 B、y1≥y2 C、y1<y2 D、y1≤y212. 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,AF平分∠CAB,交CD于点E,交CB于点F.若AC=3,AB=5,则CE的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 2014年至2016年,中国同“一带一路”沿线国家贸易总额超过3万亿美元,将3万亿美元用科学记数法表示为 .14. 化简: ÷( ﹣1)•a= .15. 某班有50名学生,平均身高为166cm,其中20名女生的平均身高为163cm,则30名男生的平均身高为cm.16. 若关于x、y的二元一次方程组 的解是 ,则ab的值为 .17. 如图,点A、B、C为⊙O上的三个点,∠BOC=2∠AOB,∠BAC=40°,则∠ACB=度.
 18. 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 .
18. 如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF.若AB=2,AD=3,则cos∠AEF的值是 . 19. 如图,一次函数y=x﹣1的图象与反比例函数y= 的图象在第一象限相交于点A,与x轴相交于点B,点C在y轴上,若AC=BC,则点C的坐标为 .
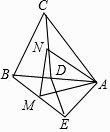
19. 如图,一次函数y=x﹣1的图象与反比例函数y= 的图象在第一象限相交于点A,与x轴相交于点B,点C在y轴上,若AC=BC,则点C的坐标为 . 20. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.
20. 如图,在△ABC与△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点D在AB上,点E与点C在AB的两侧,连接BE,CD,点M、N分别是BE、CD的中点,连接MN,AM,AN.下列结论:①△ACD≌△ABE;②△ABC∽△AMN;③△AMN是等边三角形;④若点D是AB的中点,则S△ABC=2S△ABE .
其中正确的结论是 . (填写所有正确结论的序号)
三、解答题
-
21. 有三张正面分别标有数字﹣3,1,3的不透明卡片,它们除数字外都相同,现将它们背面朝上,洗匀后从三张卡片中随机地抽取一张,放回卡片洗匀后,再从三张卡片中随机地抽取一张.(1)、试用列表或画树状图的方法,求两次抽取的卡片上的数字之积为负数的概率;(2)、求两次抽取的卡片上的数字之和为非负数的概率.22. 如图,在△ABC中,∠C=90°,∠B=30°,AD是△ABC的角平分线,DE∥BA交AC于点E,DF∥CA交AB于点F,已知CD=3.
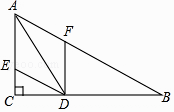 (1)、求AD的长;(2)、求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)23. 某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.(1)、求S与x之间的函数关系式,并写出自变量x的取值范围;(2)、设计费能达到24000元吗?为什么?(3)、当x是多少米时,设计费最多?最多是多少元?24. 如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.
(1)、求AD的长;(2)、求四边形AEDF的周长.(注意:本题中的计算过程和结果均保留根号)23. 某广告公司设计一幅周长为16米的矩形广告牌,广告设计费为每平方米2000元.设矩形一边长为x,面积为S平方米.(1)、求S与x之间的函数关系式,并写出自变量x的取值范围;(2)、设计费能达到24000元吗?为什么?(3)、当x是多少米时,设计费最多?最多是多少元?24. 如图,AB是⊙O的直径,弦CD与AB交于点E,过点B的切线BP与CD的延长线交于点P,连接OC,CB.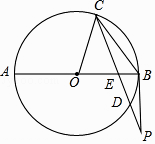 (1)、求证:AE•EB=CE•ED;(2)、若⊙O的半径为3,OE=2BE, = ,求tan∠OBC的值及DP的长.25.
(1)、求证:AE•EB=CE•ED;(2)、若⊙O的半径为3,OE=2BE, = ,求tan∠OBC的值及DP的长.25.如图,在矩形ABCD中,AB=3,BC=4,将矩形ABCD绕点C按顺时针方向旋转α角,得到矩形A'B'C'D',B'C与AD交于点E,AD的延长线与A'D'交于点F.
 (1)、
(1)、如图①,当α=60°时,连接DD',求DD'和A'F的长;
 (2)、
(2)、如图②,当矩形A'B'CD'的顶点A'落在CD的延长线上时,求EF的长;
 (3)、
(3)、如图③,当AE=EF时,连接AC,CF,求AC•CF的值.
 26.
26.如图,在平面直角坐标系中,已知抛物线y= x2+bx+c与x轴交于A(﹣1,0),B(2,0)两点,与y轴交于点C.
 (1)、求该抛物线的解析式;(2)、直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.
(1)、求该抛物线的解析式;(2)、直线y=﹣x+n与该抛物线在第四象限内交于点D,与线段BC交于点E,与x轴交于点F,且BE=4EC.①求n的值;
②连接AC,CD,线段AC与线段DF交于点G,△AGF与△CGD是否全等?请说明理由;
(3)、直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧),点 M关于y轴的对称点为点M',点H的坐标为(1,0).若四边形OM'NH的面积为 .求点H到OM'的距离d的值.
