2017年贵州省安顺市中考数学六模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 的相反数是( )A、2 B、﹣2 C、 D、﹣2. 下列计算正确的是( )A、x+x2=x3 B、x2•x3=x6 C、(x3)2=x6 D、x6÷x3=x23. 为了解某社区居民的用电情况,随机对该社区10户居民进行调查,下表是这10户居民2015年4月份用电量的调查结果:
居民(户)
1
2
3
4
月用电量(度/户)
30
42
50
51
那么关于这10户居民月用电量(单位:度),下列说法错误的是( )
A、中位数是50 B、众数是51 C、方差是42 D、极差是214.如图,AB∥CD,EF与AB、CD分别相交于点E、F,EP⊥EF,与∠EFD的平分线FP相交于点P,且∠BEP=50°,则∠EPF=( )度.
 A、70 B、65 C、60 D、555. 今年五月份香港举办“保普选反暴力”大联盟大型签名活动,9天共收集121万个签名,将121万用科学记数法表示为( )A、1.21×106 B、12.1×105 C、0.121×107 D、1.21×1056. 在Rt△ABC的直角边AC边上有一动点P(点P与点A,C不重合),过点P作直线截得的三角形与△ABC相似,满足条件的直线最多有( )A、1条 B、2条 C、3条 D、4条7. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:
A、70 B、65 C、60 D、555. 今年五月份香港举办“保普选反暴力”大联盟大型签名活动,9天共收集121万个签名,将121万用科学记数法表示为( )A、1.21×106 B、12.1×105 C、0.121×107 D、1.21×1056. 在Rt△ABC的直角边AC边上有一动点P(点P与点A,C不重合),过点P作直线截得的三角形与△ABC相似,满足条件的直线最多有( )A、1条 B、2条 C、3条 D、4条7. 如图为二次函数y=ax2+bx+c(a≠0)的图象,则下列说法:①a>0 ②2a+b=0 ③a+b+c>0 ④当﹣1<x<3时,y>0
其中正确的个数为( )
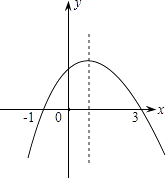 A、1 B、2 C、3 D、48. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
A、1 B、2 C、3 D、48. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( ) A、3:4 B、9:16 C、9:1 D、3:19. 如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )
A、3:4 B、9:16 C、9:1 D、3:19. 如图,将含60°角的直角三角板ABC绕顶点A顺时针旋转45°度后得到△AB′C′,点B经过的路径为弧BB′,若∠BAC=60°,AC=1,则图中阴影部分的面积是( )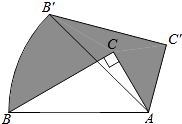 A、 B、 C、 D、π
A、 B、 C、 D、π二、填空题
-
10. 在实数范围内分解因式:x3﹣2x=11. 已知x+ =2,则 = .12. 从﹣1、0、 、0.3、π、 这六个数中任意抽取一个,抽取到无理数的概率为 .13. 已知点P(3,a)关于y轴的对称点为Q(b,2),则ab= .14. 关于x的一元二次方程x2﹣x+m=O没有实数根,则m的取值范围是 .15. 如图,在菱形ABCD中,点P是对角线AC上的一点,PE⊥AB于点E.若PE=3,则点P到AD的距离为 .
 16.
16.如图是一组有规律的图案,它们是由边长相同的正方形和正三角形镶嵌而成,第(1)个图案有4个三角形,第(2)个图案有7个三角形,第(3)个图案有10个三角形,…依此规律,第n个图案有个三角形(用含n的代数式表示)

三、解答题
-
17. 计算:(﹣2016)0+( )﹣1+| ﹣2|﹣2cos60°.18. 先化简,再求值:( +2﹣x)÷ ,其中x满足x2﹣4x+3=0.19. 某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y(微克/毫升)与服药时间x小时之间函数关系如图所示(当4≤x≤10时,y与x成反比例).
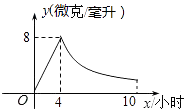 (1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.(2)、问血液中药物浓度不低于4微克/毫升的持续时间多少小时?20. ”切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时﹣﹣1.5小时;C:1.5小时﹣﹣2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,
(1)、根据图象分别求出血液中药物浓度上升和下降阶段y与x之间的函数关系式.(2)、问血液中药物浓度不低于4微克/毫升的持续时间多少小时?20. ”切实减轻学生课业负担”是我市作业改革的一项重要举措.某中学为了解本校学生平均每天的课外作业时间,随机抽取部分学生进行问卷调查,并将调查结果分为A、B、C、D四个等级,A:1小时以内;B:1小时﹣﹣1.5小时;C:1.5小时﹣﹣2小时;D:2小时以上.根据调查结果绘制了如图所示的两种不完整的统计图,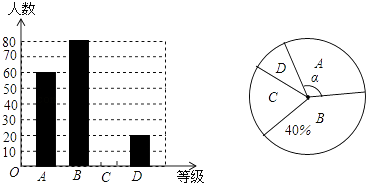
请根据图中信息解答下列问题:
(1)、该校共调查了学生;(2)、请将条形统计图补充完整;(3)、表示等级A的扇形圆心角α的度数是;(4)、在此次调查问卷中,甲、乙两班各有2人平均每天课外作业量都是2小时以上,从这4人中人选2人去参加座谈,用列表表或画树状图的方法求选出的2人来自不同班级的概率.21. “为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ≈1.41, ≈1.73)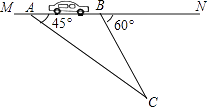 22. 某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.(1)、设A,B两种商品每件售价分别为a元、b元,求a、b的值;(2)、B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.
22. 某商场有A,B两种商品,若买2件A商品和1件B商品,共需80元;若买3件A商品和2件B商品,共需135元.(1)、设A,B两种商品每件售价分别为a元、b元,求a、b的值;(2)、B商品每件的成本是20元,根据市场调查:若按(1)中求出的单价销售,该商场每天销售B商品100件;若销售单价每上涨1元,B商品每天的销售量就减少5件.①求每天B商品的销售利润y(元)与销售单价(x)元之间的函数关系?
②求销售单价为多少元时,B商品每天的销售利润最大,最大利润是多少?
23. 如图,AB是⊙O的直径,点C是⊙O上一点,∠BAC的平分线AD交⊙O于点D,过点D垂直于AC的直线交AC的延长线于点E.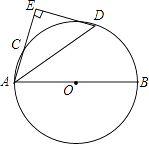 (1)、求证:DE是⊙O的切线;(2)、如果AD=5,AE=4,求AC长.24.
(1)、求证:DE是⊙O的切线;(2)、如果AD=5,AE=4,求AC长.24.如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
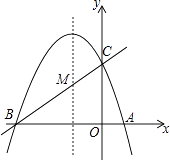 (1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
(1)、若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;(2)、在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;(3)、设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.