2017年河北省石家庄市十八县联考中考数学模拟试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 的倒数的相反数是( )A、﹣5 B、 C、﹣ D、52. 计算a12÷a4(a≠0)的结果是( )A、a3 B、a﹣8 C、a8 D、a﹣33. 使 有意义的x的取值范围是( )A、x>5 B、x≥5 C、x≠5 D、全体实数4. 如图所示的四个几何体,其中左视图与俯视图相同的几何体共有几个( )
 A、1 B、2 C、3 D、45. 化简:(a+ )(1﹣ )的结果等于( )A、a﹣2 B、a+2 C、 D、6. 多项式mx2﹣m与多项式x2﹣2x+1的公因式是( )A、x﹣1 B、x+1 C、x2﹣1 D、(x﹣1)27. 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )
A、1 B、2 C、3 D、45. 化简:(a+ )(1﹣ )的结果等于( )A、a﹣2 B、a+2 C、 D、6. 多项式mx2﹣m与多项式x2﹣2x+1的公因式是( )A、x﹣1 B、x+1 C、x2﹣1 D、(x﹣1)27. 如图,AB∥CD,∠1=58°,FG平分∠EFD,则∠FGB的度数等于( )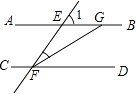 A、122° B、151° C、116° D、97°8. 若单项式2x2ya+b与﹣ xa﹣2by5的和仍然是一个单项式,则a﹣5b的立方根为( )A、﹣1 B、1 C、0 D、29. 下列说法中正确的是( )A、“任意画出一个等边三角形,它是轴对称图形”是随机事件 B、“概率为0.001的事件”是不可能事件 C、“任意画出一个平行四边形,它是中心对称图形”是必然事件 D、任意掷一枚质地均匀的硬币10次,正面向上的一定是5次10. 正比例函数的图象经过点(﹣1,2),则这个图象必须经过点( )A、(﹣2,1) B、(2,﹣1) C、(1,﹣2) D、(1,2)11. 某制药厂两年前生产1吨某种药品的成本是100万元,随着生产技术的进步,现在生产1吨这种药品的成本为81万元.设这种药品成本的年平均下降率为x,则x为( )A、3% B、6% C、8% D、10%12. 某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )A、11 B、8 C、7 D、513. 如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( )
A、122° B、151° C、116° D、97°8. 若单项式2x2ya+b与﹣ xa﹣2by5的和仍然是一个单项式,则a﹣5b的立方根为( )A、﹣1 B、1 C、0 D、29. 下列说法中正确的是( )A、“任意画出一个等边三角形,它是轴对称图形”是随机事件 B、“概率为0.001的事件”是不可能事件 C、“任意画出一个平行四边形,它是中心对称图形”是必然事件 D、任意掷一枚质地均匀的硬币10次,正面向上的一定是5次10. 正比例函数的图象经过点(﹣1,2),则这个图象必须经过点( )A、(﹣2,1) B、(2,﹣1) C、(1,﹣2) D、(1,2)11. 某制药厂两年前生产1吨某种药品的成本是100万元,随着生产技术的进步,现在生产1吨这种药品的成本为81万元.设这种药品成本的年平均下降率为x,则x为( )A、3% B、6% C、8% D、10%12. 某市出租车的收费标准是:起步价8元(即行驶距离不超过3千米都需付8元车费),超过3千米以后,每增加1千米,加收2.6元(不足1千米按1千米计),某人从甲地到乙地经过的路程是x千米,出租车费为21元,那么x的最大值是( )A、11 B、8 C、7 D、513. 如图,两同心圆的圆心为O,大圆的弦AB与小圆相切于点P,已知两圆的半径分别为2和1,用阴影部分围成一个圆锥(OA与OB重合),则该圆锥的底面半径是( ) A、 B、 C、 D、14. 如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= 位于第一象限的图象上,则k的值为( )
A、 B、 C、 D、14. 如图,在平面直角坐标系中,边长为6的正六边形ABCDEF的对称中心与原点O重合,点A在x轴上,点B在反比例函数y= 位于第一象限的图象上,则k的值为( ) A、9 B、9 C、3 D、315. 如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( )
A、9 B、9 C、3 D、315. 如图所示的运算程序中,若开始输入的x值为15,则第1次输出的结果为18,第2次输出的结果为9,…,第2017次输出的结果为( ) A、3 B、4 C、6 D、916. 如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )
A、3 B、4 C、6 D、916. 如图,Rt△ABC中∠C=90°,∠BAC=30°,AB=8,以2 为边长的正方形DEFG的一边GD在直线AB上,且点D与点A重合,现将正方形DEFG沿A﹣B的方向以每秒1个单位的速度匀速运动,当点D与点B重合时停止,则在这个运动过程中,正方形DEFG与△ABC的重合部分的面积S与运动时间t之间的函数关系图象大致是( )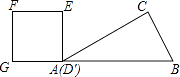 A、
A、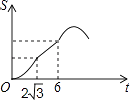 B、
B、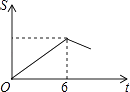 C、
C、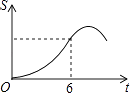 D、
D、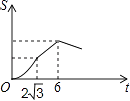
二、填空题
-
17. 写出一个比4小的正无理数 .18. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2 . 则OC的长为 cm.
 19. 某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .
19. 某学校计划购买A、B两种品牌的显示器共120台,A、B两种品牌显示器的单价分别为800元和1000元,设购买A品牌显示器x台,若学校购买这两种品牌显示器的总费用为110000元,那么A、B两种品牌的显示器各购买了多少台?根据题目信息完成上面的表格,并列出方程,列出的方程: .项目
品牌
单价/元
购买数量/台
购买费用/元
A
800
x
B
1000
三、解答题
-
20. 综合题。(1)、计算:(3﹣π)0﹣ +|3﹣ |+(tan30°)﹣1(2)、定义新运算:对于任意实数a,b,都有a⊕b=a(a﹣b)+1,等式右边是通常的加法、减法及乘法运算.
比如:2⊕5=2×(2﹣5)+1
=2×(﹣3)+1
=﹣6+1
=﹣5
若3⊕x的值小于13,求x的取值范围,并在如图所示的数轴上表示出来.
 21. 在不透明的布袋中装有1个白球,2个红球,它们除颜色外其余完全相同.(1)、从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个红球的概率;(2)、若在布袋中再添加x个白球,充分搅匀,从中摸出一个球,使摸到白球的概率为 ,求添加的白球个数x.22. 如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°.
21. 在不透明的布袋中装有1个白球,2个红球,它们除颜色外其余完全相同.(1)、从袋中任意摸出两个球,试用树状图或表格列出所有等可能的结果,并求摸出的球恰好是两个红球的概率;(2)、若在布袋中再添加x个白球,充分搅匀,从中摸出一个球,使摸到白球的概率为 ,求添加的白球个数x.22. 如图1所示,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD,以AD为直角边,A为直角顶点,在AD左侧作等腰直角三角形ADF,连接CF,AB=AC,∠BAC=90°. (1)、当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.(2)、当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由.
(1)、当点D在线段BC上时(不与点B重合),线段CF和BD的数量关系与位置关系分别是什么?请给予证明.(2)、当点D在线段BC的延长线上时,(1)的结论是否仍然成立?请在图2中画出相应的图形,并说明理由. 23. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数y= 的图象上.
23. 如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点C,点A( ,1)在反比例函数y= 的图象上. (1)、求k的值;(2)、若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.24. 阅读下列材料:
(1)、求k的值;(2)、若将△BOA绕点B按逆时针方向旋转60°,得到△BDE,判断点E是否在该反比例函数的图象上,并说明理由.24. 阅读下列材料:如图1,圆的概念:在平面内,线段PA绕它固定的一个端点P旋转一周,另一个端点A所形成的图形叫做圆.就是说,到某个定点等于定长的所有点在同一个圆上,圆心在P(a,b),半径为r的圆的方程可以写为:(x﹣a)2+(y﹣b)2=r2 , 如:圆心在P(2,﹣1),半径为5的圆方程为:(x﹣2)2+(y+1)2=25
 (1)、填空:
(1)、填空:①以A(3,0)为圆心,1为半径的圆的方程为;
②以B(﹣1,﹣2)为圆心, 为半径的圆的方程为 .
(2)、根据以上材料解决下列问题:如图2,以B(﹣6,0)为圆心的圆与y轴相切于原点,C是⊙B上一点,连接OC,作BD⊥OC垂足为D,延长BD交y轴于点E,已知sin∠AOC= .

①连接EC,证明EC是⊙B的切线;
②在BE上是否存在一点P,使PB=PC=PE=PO?若存在,求P点坐标,并写出以P为圆心,以PB为半径的⊙P的方程;若不存在,说明理由.
25. 如图,已知抛物线经过原点O和x轴上另一点A,它的对称轴x=2与x轴交于点C,直线y=﹣2x﹣1经过抛物线上一点B(﹣2,m),且与y轴、直线x=2分别交于点D、E. (1)、求m的值及该抛物线对应的函数关系式;(2)、判断直线BE与抛物线交点的个数;(3)、求证:CD垂直平分BE;(4)、若P是该抛物线上的一个动点,是否存在这样的点P,使得△PBE是等腰直角三角形,且∠PEB=90°?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.26. 如图1所示,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).
(1)、求m的值及该抛物线对应的函数关系式;(2)、判断直线BE与抛物线交点的个数;(3)、求证:CD垂直平分BE;(4)、若P是该抛物线上的一个动点,是否存在这样的点P,使得△PBE是等腰直角三角形,且∠PEB=90°?若存在,试求出所有符合条件的点P的坐标;若不存在,请说明理由.26. 如图1所示,在▱ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).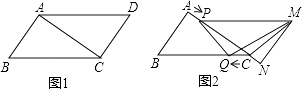 (1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
(1)、当t为何值时,PQ∥MN?(2)、设△QMC的面积为y(cm2),求y与t之间的函数关系式;(3)、是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.