2017年河北省廊坊市安次区中考数学二模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 计算（﹣3）×|﹣2|的结果等于（）

A、6 B、5 C、﹣6 D、﹣5

查看试题解析
2. 2cos45°的值等于（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\sqrt{2}$ C、 $\frac{\sqrt{2}}{4}$ D、2 $\sqrt{2}$

查看试题解析
3. 下列几何图形中，对称性与其它图形不同的是（）

A、 B、 C、 D、

查看试题解析
4. 实数 $\sqrt{41}$ 的小数部分是（）

A、6﹣ $\sqrt{41}$ B、 $\sqrt{41}$ ﹣6 C、7﹣ $\sqrt{41}$ D、 $\sqrt{41}$ ﹣7

查看试题解析
5. 把a²﹣4a多项式分解因式，结果正确的是（　　）

A、a（a﹣4） B、（a+2）（a﹣2） C、a（a+2）（a﹣2） D、（a﹣2）²﹣4

查看试题解析
6. 如果式子 $\sqrt{2 x + 6}$ 有意义，那么x的取值范围在数轴上表示出来，正确的是（）

A、 B、 C、 D、

查看试题解析
7. 若关于x的方程x²+2x+a=0不存在实数根，则a的取值范围是（　　）.

A、a＜1 B、a＞1 C、a≤1 D、a≥1

查看试题解析
8. 小王参加某企业招聘测试，他的笔试、面试、技能操作得分分别为85分、80分、90分，若依次按照2：3：5的比例确定成绩，则小王的成绩是（）

A、255分 B、84分 C、84.5分 D、86分

查看试题解析
9. 如图，正六边形螺帽的边长是2cm，这个扳手的开口a的值应是（）

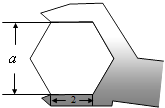A、 $2 \sqrt{3}$ cm B、 $\sqrt{3}$ cm C、 $\frac{2 \sqrt{3}}{3}$ cm D、1cm

查看试题解析
10. 如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC的度数是（）

A、35° B、55° C、65° D、70°

查看试题解析
11. 如图，一个多边形纸片按图示的剪法剪去一个内角后，得到一个内角和为2340°的新多边形，则原多边形的边数为（）

A、13 B、14 C、15 D、16

查看试题解析
12. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E．若BF=6，AB=5，则AE的长为（　　）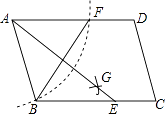

A、4 B、6 C、8 D、10

查看试题解析
13. 如图，直线l：y=﹣ $\frac{2}{3}$ x﹣3与直线y=a（a为常数）的交点在第四象限，则a可能在（）

A、1＜a＜2 B、﹣2＜a＜0 C、﹣3≤a≤﹣2 D、﹣10＜a＜﹣4

查看试题解析
14.
如图，在直角∠O的内部有一滑动杆AB，当端点A沿直线AO向下滑动时，端点B会随之自动地沿直线OB向左滑动，如果滑动杆从图中AB处滑动到A′B′处，那么滑动杆的中点C所经过的路径是（）

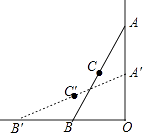A、直线的一部分 B、圆的一部分 C、双曲线的一部分 D、抛物线的一部分

查看试题解析
15. 如图，△ABC的面积为6，AC=3，现将△ABC沿AB所在直线翻折，使点C落在直线AD上的C′处，P为直线AD上的一点，则线段BP的长不可能是（）

A、3 B、4 C、5.5 D、10

查看试题解析
16. 如图a，有两个全等的正三角形ABC和DEF，点D、C分别为△ABC、DEF的内心；固定点D，将△DEF顺时针旋转，使得DF经过点C，如图b，则图a中四边形CNDM与图b中△CDM面积的比为（）

A、2：1 B、2： $\sqrt{3}$ C、4：3 D、 $\sqrt{3}$ ： $\sqrt{2}$

查看试题解析

二、填空题

17. 计算：（﹣1）⁰+|﹣1|= ．

查看试题解析
18. 老师在黑板上书写了一个正确的演算过程，随后用手掌捂住了一个二次三项式，形式如下：
﹣3x=x²﹣5x+1，若x= $\sqrt{6} + 1$ ，则所捂二次三项式的值为．

查看试题解析
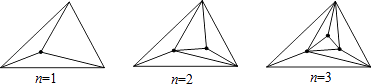
19.
一个三角形内有n个点，在这些点及三角形顶点之间用线段连接起来，使得这些线段互不相交，且又能把原三角形分割为不重叠的小三角形．如图：若三角形内有1个点时此时有3个小三角形；若三角形内有2个点时，此时有5个小三角形．则当三角形内有3个点时，此时有个小三角形；当三角形内有n个点时，此时有个小三角形．

查看试题解析

三、解答题

20. 已知A= $\frac{x^{2} + 2 x + 1}{x^{2} - 1}$ ﹣ $\frac{x}{x - 1}$

(1)、化简A；

(2)、当x满足不等式组 ${\begin{matrix} x - 1 \geq 0 \\ x - 3 < 0 \end{matrix}$ ，且x为整数时，求A的值．

查看试题解析
21. 如图，在▱ABCD中，对角线AC，BD相交于点O，AB=5，AC=6，BD=8．

(1)、求证：四边形ABCD是菱形；

(2)、过点A作AH⊥BC于点H，求AH的长．

查看试题解析
22. 某电视台在它的娱乐性节目中每期抽出两名场外幸运观众，有一期甲、乙两人被抽为场外幸运观众，他们获得了一次抽奖的机会，在如图所示的翻奖牌的正面4个数字中任选一个，选中后翻开，可以得到该数字反面的奖品，第一个人选中的数字第二个人不能再选择了．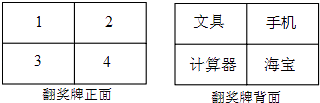

(1)、如果甲先抽奖，那么甲获得“手机”的概率是多少？

(2)、小亮同学说：甲先抽奖，乙后抽奖，甲、乙两人获得“手机”的概率不同，且甲获得“手机”的概率更大些．你同意小亮同学的说法吗？为什么？请用列表或画树状图分析．

查看试题解析
23.
小敏家对面新建了一幢图书大厦，小敏在自家窗口测得大厦顶部的仰角为45°，大厦底部的仰角为30°，如图所示，量得两幢楼之间的距离为20 $\sqrt{3}$ 米．

(1)、求出大厦的高度BD；

(2)、求出小敏家的高度AE．

查看试题解析
24. 某采摘农场计划种植A，B两种草莓共6亩，根据表格信息，解答下列问题：
项目品种
A
B
年亩产（单位：千克）
1200
2000
采摘价格
（单位：元/千克）
60
40

(1)、若该农场每年草莓全部被采摘的总收入为460000元，那么A、B两种草莓各种多少亩？

(2)、若要求种植A种草莓的亩数不少于种植B种草莓的一半，那么种植A种草莓多少亩时，可使该农场每年草莓全部被采摘的总收入最多？并求出最多总收入．

查看试题解析
25. 已知：线段CB=6，点A在线段BC上，且CA=2，以AB为直径做半圆O，点D为半圆O上的动点，以CD为边向外作等边△CDE．

(1)、发现：CD的最小值是，最大值是， △CBD面积的最大值是．

(2)、思考：如图1，当线段CD所在直线与半圆O相切时，求弧BD的长．

(3)、探究：如图2，当线段CD与半圆O有两个公共点D，M时，若CM=DM，求等边△CDE面积．

查看试题解析
26.
如图，已知抛物线y=x²﹣2bx﹣3（b为常数，b＜0）．

(1)、抛物线y=x²﹣2bx﹣3总经过一定点，定点坐标为；

(2)、抛物线的对称轴为直线x=（用含b的代数式表示），位于y轴的
侧．

(3)、思考：若点P（﹣2，﹣1）在抛物线y=x²﹣2bx﹣3上，抛物线与反比例函数y= $\frac{k}{x}$ （k＞0，x＞0）的图象在第一象限内交点的横坐标为a，且满足2＜a＜3，试确定k的取值范围．

(4)、探究：设点A是抛物线上一点，且点A的横坐标为m，以点A为顶点做边长为1的正方形ABCD，AB⊥x轴，点C在点A的右下方，若抛物线与CD边相交于点P（不与D点重合且不在y轴上），点P的纵坐标为﹣3，求b与m之间的函数关系式．

查看试题解析