2017年广东省广州市增城区中考数学一模试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、选择题
-
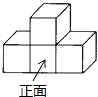
1. 比0小的数是（ ）A、﹣8 B、8 C、±8 D、2. 如图所示的几何体是由四个完全相同的正方体组成的，这个几何体的俯视图是（ ）
A、
B、
C、
D、
3. 如图，将面积为5的△ABC沿BC方向平移至△DEF的位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积为（ ）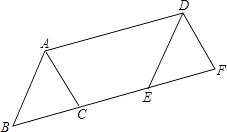
A、5 B、10 C、15 D、204. 计算：（a2b）3的结果是（ ）A、a6b B、a6b3 C、a5b3 D、a2b35. 下列说法正确的是（ ）A、一个游戏中奖的概率是 ，则做100次这样的游戏一定会中奖 B、为了了解全国中学生的心理健康状况，应采用普查的方式 C、一组数据0，1，2，1，1的众数和中位数都是1 D、若甲组数据的方差S甲2=0.2，乙组数据的方差S乙2=0.5，则乙组数据比甲组数据稳定6. 不等式组 的解集是（ ）A、﹣2≤x≤1 B、﹣2＜x＜1 C、x≤﹣1 D、x≥27. 若a＜1，化简 ﹣1=（ ）A、a﹣2 B、2﹣a C、a D、﹣a8. 若代数式 有意义，则实数x的取值范围是（ ）A、x≠2 B、x≥0 C、x＞0 D、x≥0且x≠29. 已知α，β是一元二次方程x2﹣5x﹣2=0的两个实数根，则α2+αβ+β2的值为（ ）A、﹣1 B、9 C、23 D、2710. 如图，边长分别为4和8的两个正方形ABCD和CEFG并排放在一起，连结BD并延长交EG于点T，交FG于点P，则GT=（ ）
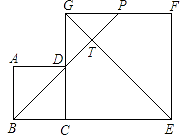A、 B、2 C、2 D、1二、填空题
-
11. 分解因式：x2﹣4x= ．
12. 增城区城市副中心核心区规划面积是64000000平方米，将64000000用科学记数法表示为 ．13. 反比例函数y= ，若x＞0时，y随x的增大而增大，则m的取值范围是 ．14. 点P在线段AB的垂直平分线上，PB=10，则PA= ．15. 如图，在等边△ABC中，AB=10，D是BC的中点，将△ABD绕点A旋转后得到△ACE，则线段DE的长度为 ．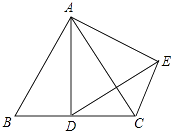
16. 如图，AB是⊙O的直径，C、D是⊙O上的点，∠CDB=30°，过点C作⊙O的切线交AB的延长线于E，则sinE的值为 ．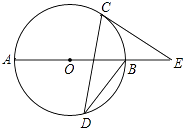
三、解答题
-
17. 先化简，再求值： ，其中 ．18. 解方程组 ．19. 在Rt△ABC中，∠ACB=90°，CD⊥AB于D，AC=20，BC=15，
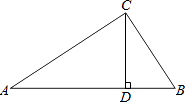(1)、求AB的长；(2)、求CD的长．20. 如图，在△ABC中，AB=AC，D是BA延长线上一点，E是AC的中点．
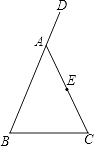(1)、利用尺规作出∠DAC的平分线AM，连接BE并延长交AM于点F，（要求在图中标明相应字母，保留作图痕迹，不写作法）；(2)、试判断AF与BC有怎样的位置关系与数量关系，并说明理由．21. 小明对自己所在班级的50名学生平均每周参加课外活动的时间进行了调查，由调查结果绘制了频数分布直方图，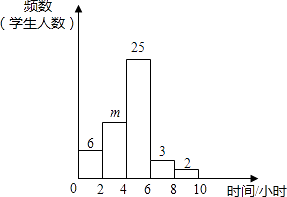
根据图中信息回答下列问题：
(1)、求m的值；(2)、从参加课外活动时间在6～10小时的5名学生中随机选取2人，请你用列表或画树状图的方法，求其中至少有1人课外活动时间在8～10小时的概率．22. 在Rt△ABC中，∠ACB=90°，D是AB边上的一点，以BD为直径作⊙O交AC于点E，连结DE并延长，与BC的延长线交于点F．且BD=BF．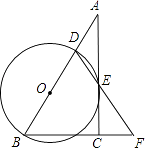
(1)、求证：AC与⊙O相切．(2)、若BC=6，AB=12，求⊙O的面积．23. 如图，制作某金属工具先将材料煅烧6分钟温度升到800℃，再停止煅烧进行锻造，8分钟温度降为600℃；煅烧时温度y（℃）与时间x（min）成一次函数关系；锻造时温度y（℃）与时间x（min）成反比例函数关系；该材料初始温度是32℃．
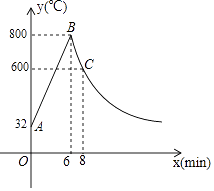(1)、分别求出材料煅烧和锻造时y与x的函数关系式；(2)、根据工艺要求，当材料温度低于480℃时，须停止操作，那么锻造的操作时间有多长？
