2017年广西玉林市中考数学二模试卷
试卷更新日期:2017-07-24 类型:中考模拟
一、选择题
-
1. 2的相反数是( )A、﹣2 B、2 C、 D、2. 把0.0000052用科学记数法表示为( )A、0.52×10﹣5 B、5.2×10﹣5 C、5.2×10﹣6 D、52×10﹣53. 如图,是轴对称图形但不是中心对称图形的是( )A、
 线段
B、
线段
B、 等边三角形
C、
等边三角形
C、 正方形
D、
正方形
D、 圆
4. 下列运算正确的是( )A、2a2+3a3=5a5 B、a6÷a3=a2 C、(﹣a3)2=a6 D、(x+y)2=x2+y25. 如图是由八个相同小正方体组合而成的几何体,则其俯视图是( )
圆
4. 下列运算正确的是( )A、2a2+3a3=5a5 B、a6÷a3=a2 C、(﹣a3)2=a6 D、(x+y)2=x2+y25. 如图是由八个相同小正方体组合而成的几何体,则其俯视图是( )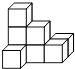 A、
A、 B、
B、 C、
C、 D、
D、 6. 2015年1月份,无锡市某周的日最低气温统计如下表,则这七天中日最低气温的众数和中位数分别是( )
6. 2015年1月份,无锡市某周的日最低气温统计如下表,则这七天中日最低气温的众数和中位数分别是( )日期
19
20
21
22
23
24
25
最低气温/℃
2
4
5
3
4
6
7
A、4,4 B、5,4 C、4,3 D、4,4.57. 分式方程 ﹣ =2的解是( )A、x=﹣1 B、x=1 C、x=﹣2 D、x=28. 某班学校毕业时,每个同学都要给其他同学写一份毕业留言作为纪念,全班学生共写了2550份留言,如果全班有x名学生,根据题意,列出方程( )A、 =2550 B、 =2550 C、x(x﹣1)=2550 D、x(x+1)=25509. 如图,沿AE折叠矩形纸片ABCD,使点D落在BC边的点F处已知AB=8,BC=10,则tan∠EFC的值为( )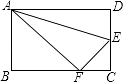 A、 B、 C、 D、10.
A、 B、 C、 D、10.在湖边高出水面50m的山顶A处看见一艘飞艇停留在湖面上空某处,观察到飞艇底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则飞艇底部P距离湖面的高度为(参考等式: = )( )
 A、25 +75 B、50 +50 C、75 +75 D、50 +10011. 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y= 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )
A、25 +75 B、50 +50 C、75 +75 D、50 +10011. 如图,两个边长分别为a,b(a>b)的正方形连在一起,三点C,B,F在同一直线上,反比例函数y= 在第一象限的图象经过小正方形右下顶点E.若OB2﹣BE2=10,则k的值是( )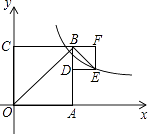 A、3 B、4 C、5 D、4
A、3 B、4 C、5 D、4二、填空题
-
12. ﹣7的绝对值是 .13. 分解因式:ax2﹣4ax+4a=14. 在一个不透明的盒子里装有3个分别标有数字1,2,3的小球,它们除数字外其他均相同,充分摇匀后,先摸出1个球不放回,再摸出1个球,那么这两个球上的数字之和为奇数的概率为 .15. 如图所示,在四边形ABCD中,AB∥CD,AD⊥CD,点E、F分别是AB,BC的中点,AB=4,EF=2,∠B=60°,则CD的长为 .
 16. 如图,若将平面直角坐标系中“鱼”以原点O为位似中心,按照相似比 缩小,则点A的对应点的坐标是 .
16. 如图,若将平面直角坐标系中“鱼”以原点O为位似中心,按照相似比 缩小,则点A的对应点的坐标是 . 17. 在一次猜数字游戏中,小红写出如下一组数:1, , , , …,小军猜想出的第六个数字是 ,也是正确的,根据此规律,第n个数是 .
17. 在一次猜数字游戏中,小红写出如下一组数:1, , , , …,小军猜想出的第六个数字是 ,也是正确的,根据此规律,第n个数是 .三、解答题
-
18. 计算: +2﹣1﹣( ﹣ )0 .19. 化简分式 ÷ ﹣1,并选取一个你认为合适的整数a代入求值.20. 已知关于x的一元二次方程x2﹣6x+2m+1=0有实数根.(1)、求实数m的取值范围;(2)、若方程的两个实数根为x1 , x2 , 且x1x2+x1+x2=15,求m的值.21. 某科学技术协会为倡导青少年主动进行研究性学习,积极研究身边的科学问题,组织了以“体验、创新、成长”为主题的青少年科技创大赛,在层层选拔的基础上,所有推荐参赛学生分别获得了一、二、三等奖和纪念奖,工作人员根据获奖情况绘制成如图所示的两幅不完整的统计图,根据图中所给出的信息解答下列问题:
 (1)、这次大赛获得三等奖的学生有多少人?(2)、请将条形统计图补充完整;(3)、扇形统计图中,表示三等奖扇形的圆心角是多少度?(4)、若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.22. 如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2 .
(1)、这次大赛获得三等奖的学生有多少人?(2)、请将条形统计图补充完整;(3)、扇形统计图中,表示三等奖扇形的圆心角是多少度?(4)、若给所有推荐参赛学生每人发一张相同的卡片,各自写上自己的名字,然后把卡片放入一个不透明的袋子里,摇匀后任意摸出一张,求摸出写有一等奖学生名字卡片的概率.22. 如图,AB是⊙O的直径,C为⊙O上一点,点D在CO的延长线上,连接BD,已知BC=BD,AB=4,BC=2 . (1)、求证:BD是⊙O的切线;(2)、求CD的长.23. 2013年1月,由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:
(1)、求证:BD是⊙O的切线;(2)、求CD的长.23. 2013年1月,由于雾霾天气持续笼罩我国中东部大部分地区,口罩市场出现热卖,某旗舰网店用8000元购进甲、乙两种口罩,销售完后共获利2800元,进价和售价如下表:品名
价格
甲种口罩
乙种口罩
进价(元/袋)
20
25
售价(元/袋)
26
35
(1)、求该网店购进甲、乙两种口罩各多少袋?(2)、该网店第二次以原价购进甲、乙、两种口罩,购进乙种口罩袋数不变,而购进甲种口罩袋数是第一次的2倍.甲种口罩按原售价出售,而乙种口罩让利销售.若两种口罩销售完毕,要使第二次销售活动获利不少于3680元,乙种口罩最低售价为每袋多少元?

