2017年广东省中考数学学业信息试卷（一）

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 在﹣3，1，π，0.35 中，无理数是（）

A、﹣3 B、 $\frac{1}{2}$ C、π D、0.35

查看试题解析
2. 根据有关资料显示，2015年广东省财政收入约为20934亿元，突破2万亿大关，财政支出民生实事类占近七成，数据20934亿用科学记数法表示为（）

A、2.0934×10¹² B、2.0934×10¹³ C、20.934×10¹¹ D、20934×10⁸

查看试题解析
3. 如图是由四个完全相同的正方体组成的几何体，这个几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 计算（﹣2a²）²•a，正确的是（）

A、2a⁵ B、﹣4a⁵ C、4a⁵ D、4a⁶

查看试题解析
5. 从分别标有数﹣3，﹣2，﹣1，1，2，3的六张没有明显差别的卡片中，随机抽取一张，所抽卡片上的数均大于﹣2的概率是（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
6. 若一个正多边形的一个外角是45°，则这个正多边形的边数是（）

A、10 B、9 C、8 D、6

查看试题解析
7. 下列性质中，菱形具有而平行四边形不具有的性质是（）

A、对边平行且相等 B、对角线互相平分 C、对角线互相垂直 D、对角互补

查看试题解析
8. 如果关于x的一元二次方程2x²﹣x+k=0有两个实数根，那么k的取值范围是（）

A、k≥ $\frac{1}{8}$ B、k≤ $\frac{1}{8}$ C、k≥﹣ $\frac{1}{8}$ D、k≤﹣ $\frac{1}{8}$

查看试题解析
9. 三角板ABC中，∠ACB=90°，∠B=30°，AC=2 $\sqrt{3}$ ，三角板绕直角顶点C逆时针旋转，当点A的对应点A′落在AB边的起始位置上时即停止转动，则B点转过的路径长为（）

A、 $\frac{3}{2}$ π B、 $\frac{4}{3} \sqrt{3}$ π C、2π D、3π

查看试题解析
10. 如图，△ABC是边长为4cm的等边三角形，动点P从点A出发，以2cm/s的速度沿A→C→B运动，到达B点即停止运动，过点P作PD⊥AB于点D，设运动时间为x（s），△ADP的面积为y（cm²），则能够反映y与x之间函数关系的图象大致是（）

A、 B、 C、 D、

查看试题解析

二、填空题

11. 因式分解：m²﹣4n²= ．

查看试题解析
12. （ $\sqrt{2}$ ﹣1.414）⁰+（ $\frac{1}{3}$ ）^﹣¹﹣ $\sqrt{27}$ +2cos30°= ．

查看试题解析
13. 如图，在△ABC中，AB=AC，AD⊥BC，垂足为D，E是AC中点，若DE=2，则AB的长为．

查看试题解析
14. 如图，点O是⊙O的圆心，点A、B、C在⊙O上，AO∥BC，∠AOB=42°，则∠OAC的度数是．

查看试题解析
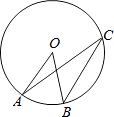15. 将直角边长为5cm的等腰直角△ABC绕点A逆时针旋转15°后，得到△AB′C′，则图中阴影部分的面积是 cm² ．

查看试题解析
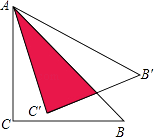16. 如图，折叠矩形ABCD的一边AD，使点D落在BC边的点F处，已知折痕AE=5 $\sqrt{5}$ cm，且tan∠EFC= $\frac{3}{4}$ ，则矩形ABCD的周长是．

查看试题解析

三、解答题

17. 解不等式组： ${\begin{matrix} 2 x + 3 < 9 - x \\ 2 x - 5 > 10 - 3 x \end{matrix}$ ．

查看试题解析
18. 先化简，再求值：（1+ $\frac{1}{x - 1}$ ）÷ $\frac{2 x}{x^{2} - 1}$ ，其中x= $\sqrt{2}$ ﹣1．

查看试题解析
19. 如图，AE∥BF，AC平分∠BAE，交BF于C．

(1)、尺规作图：过点B作AC的垂线，交AC于O，交AE于D，（保留作图痕迹，不写作法）；

(2)、求证：AD=BC．

查看试题解析
20. 为了抓住文化艺术节的商机，某商店决定购进A、B两种艺术节纪念品．若购进A种纪念品8件，B种纪念品3件，需要950元；若购进A种纪念品5件，B种纪念品6件，需要800元．

(1)、求购进A、B两种纪念品每件各需多少元？

(2)、若该商店决定购进这两种纪念品共100件，考虑市场需求和资金周转，用于购买这100件纪念品的资金不超过8 000元，那么该商店至多购进A种纪念品几件？

查看试题解析
21. 为了解本校九年级学生期末数学考试情况，小亮在九年级随机抽取了一部分学生的期末数学成绩为样本，分为A（100﹣90分）、B（89～80分）、C（79～60分）、D（59～0分）四个等级进行统计，并将统计结果绘制成如下统计图，请你根据统计图解答以下问题：

(1)、这次随机抽取的学生共有多少人？

(2)、请补全条形统计图；

(3)、这个学校九年级共有学生1200人，若分数为80分（含80分）以上为优秀，请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少？

查看试题解析
22. 如图，河的两岸l₁与l₂相互平行，A、B是l₁上的两点，C、D是l₂上的两点，某人在点A处测得∠CAB=90°，∠DAB=30°，再沿AB方向前进60米到达点E（点E在线段AB上），测得∠DEB=60°，求河的宽度．

查看试题解析
23.
如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ （x＞0）的图象交于点P（n，2），与x轴交于点A（﹣4，0），与y轴交于点C，PB⊥x轴于点B，点A与点B关于y轴对称．

(1)、求一次函数，反比例函数的解析式；

(2)、求证：点C为线段AP的中点；

(3)、反比例函数图象上是否存在点D，使四边形BCPD为菱形？如果存在，说明理由并求出点D的坐标；如果不存在，说明理由．

查看试题解析
24. 如图，AB为⊙O直径，BC为⊙O切线，连接A、C两点，交⊙O于点D，BE=CE，连接DE，OE．

(1)、判断DE与⊙O的位置关系，并说明理由；

(2)、求证：BC²=CD•2OE；

(3)、若cos∠BAD= $\frac{3}{5}$ ，BE=6，求OE的长．

查看试题解析
25.
如图，在Rt△ABC中，∠B=90°，直线EF分别交两直角边AB、BC与E、F两点，且EF∥AC，P是斜边AC的中点，连接PE，PF，且AB= $\frac{6}{5}$ ，BC= $\frac{8}{5}$ ．

(1)、当E、F均为两直角边的中点时，求证：四边形EPFB是矩形，并求出此时EF的长；

(2)、设EF的长度为x（x＞0），当∠EPF=∠A时，用含x的代数式表示EP的长；

(3)、设△PEF的面积为S，则当EF为多少时，S有最大值，并求出该最大值．

查看试题解析