2017年广东省深圳市南山区中考数学三模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 某小镇在2017年常住人口达到25.8万，用科学记数法表示应为（）

A、25.8×10⁴ B、25.8×10⁵ C、2.58×10⁵ D、2.58×10⁶

查看试题解析
2. 下列运算中，正确的是（）

A、x³+x³=x⁶ B、x³•x⁹=x²⁷ C、（x²）³=x⁵ D、x÷x²=x^﹣¹

查看试题解析
3. 函数y= $\frac{1}{x + 1}$ 中自变量x的取值范围是（）

A、x≥﹣1 B、x≤﹣1 C、x≠﹣1 D、x=﹣1

查看试题解析
4. $\sqrt{16}$ 的平方根是（）

A、±2 B、2 C、﹣2 D、16

查看试题解析
5. 数据6，8，8，x的众数有两个，则这组数据的中位数是（）

A、6 B、7 C、8 D、9

查看试题解析
6. 在平面直角坐标系中，若点P（m﹣3，m+1）在第二象限，则m的取值范围为（　　）

A、﹣1＜m＜3 B、m＞3 C、m＜﹣1 D、m＞﹣1

查看试题解析
7. 如图，是一个由若干个相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体的个数是（）

A、7个 B、8个 C、9个 D、10个

查看试题解析
8. 若A（﹣1，y₁），B（﹣5，y₂），C（0，y₃）为二次函数y=x²+4x﹣5的图象上的三点，则y₁ ， y₂ ， y₃的大小关系是（）

A、y₁＜y₂＜y₃ B、y₂＜y₁＜y₃ C、y₃＜y₁＜y₂ D、y₁＜y₃＜y₂

查看试题解析
9. 如图，扇形纸扇完全打开后，外侧两竹条AB，AC夹角为120°，AB的长为30cm，贴纸部分BD的长为20cm，则贴纸部分的面积为（）

A、100πcm² B、 $\frac{400}{3}$ πcm² C、800πcm² D、 $\frac{800}{3}$ πcm²

查看试题解析
10. 根据函数y= $\frac{1}{x}$ 的图象，判断当x≥﹣1时，y的取值范围是（）

A、y＜﹣1 B、y≤﹣1 C、y≤﹣1或y＞0 D、y＜﹣1或y≥0

查看试题解析
11. 如图，小明随意向水平放置的大正方形内部区域抛一个小球，则小球停在小正方形内部（阴影）区域的概率为（）

A、 $\frac{3}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{1}{4}$

查看试题解析
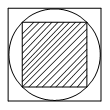12. 如图，△ABC内接于⊙O，∠A的度数为60°，∠ABC、∠ACB的角平分线分别交于AC、AB于点D、E，CE、BD相交于点F．以下四个结论：①cos∠BFE= $\frac{1}{2}$ ；②BC=BD；③EF=FD；④BF=2DF．其中结论一定正确的序号数是（）

A、①② B、①③ C、③④ D、②④

查看试题解析

二、填空题

13. 分解因式：x³﹣6x²+9x= ．

查看试题解析
14. 某书店把一本新书按标价的九折出售，仍可获利20%．若该书的进价为21元，则标价为元．

查看试题解析
15. 如图中每个阴影部分是以多边形各顶点为圆心，1为半径的扇形，并且所有多边形的每条边长都＞2，则第n个多边形中，所有扇形面积之和是．（结果保留π）

查看试题解析
16. 如图，矩形AOCB的两边OC、OA分别位x轴、y轴上，点B的坐标为B（ $- \frac{20}{3}$ ，5），D是AB边上的一点．将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式是．

查看试题解析

三、解答题

17. 计算：2^﹣¹﹣tan60°+（ $\sqrt{5}$ ﹣1）⁰﹣|2﹣ $\sqrt{3}$ |．

查看试题解析
18. 解方程： $\frac{a - b}{a + 2 b}$ ÷ $\frac{a^{2} - b^{2}}{a^{2} + 4 a b + 4 b^{2}}$ ﹣1，其中a=3+ $\sqrt{5}$ ，b=3﹣ $\sqrt{5}$ ．

查看试题解析
19. 如图，把一张矩形的纸ABCD沿对角线BD折叠，使点C落在点E处，BE与AD交于点F．

(1)、求证：△ABF≌△EDF；

(2)、若将折叠的图形恢复原状，点F与BC边上的点M正好重合，连接DM，试判断四边形BMDF的形状，并说明理由．

查看试题解析
20. 学习了统计知识后，班主任王老师叫班长就本班同学的上学方式进行了一次调查统计，图1和图2是他通过收集数据后，绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：

(1)、在扇形统计图中，计算出“步行”部分所对应的圆心角的度数；

(2)、求该班共有多少名学生；

(3)、在图1中，将表示“乘车”的部分补充完整．

查看试题解析
21. 某公司试销一种成本为30元/件的新产品，按规定试销时的销售单价不低于成本单价，又不高于80元/件，试销中每天的销售量y（件）与销售单价x（元/件）满足下表中的函数关系．
x（元/件）
35
40
45
50
55
y（件）
550
500
450
400
350

(1)、试求y与x之间的函数表达式；

(2)、设公司试销该产品每天获得的毛利润为S（元），求S与x之间的函数表达式（毛利润=销售总价﹣成本总价）；

(3)、当销售单价定为多少时，该公司试销这种产品每天获得的毛利润最大？最大毛利润是多少？此时每天的销售量是多少？

查看试题解析
22.
如图，二次函数y=ax²的图象与一次函数y=x+b的图象相交于A（﹣2，2）、B两点，从点A和点B分别引平行于y轴的直线与x轴分别交于C，D两点，点P（t，0），为线段CD上的动点，过点P且平行于y轴的直线与抛物线和直线分别交于R，S．

(1)、求一次函数和二次函数的解析式，并求出点B的坐标；

(2)、当SR=2RP时，计算线段SR的长；

(3)、若线段BD上有一动点Q且其纵坐标为t+3，问是否存在t的值，使S_△_BRQ=15？若存在，求t的值；若不存在，说明理由．

查看试题解析
23.
在△ABC中，∠A=90°，AB=4，AC=3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM=x．

(1)、用含x的代数式表示△MNP的面积S；

(2)、当x为何值时，⊙O与直线BC相切；

(3)、在动点M的运动过程中，记△MNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式，并求x为何值时，y的值最大，最大值是多少？

查看试题解析

x（元/件）	35	40	45	50	55
y（件）	550	500	450	400	350