2017年福建省莆田市仙游县第六片区中考数学模拟试卷
试卷更新日期：2017-07-24 类型：中考模拟
一、精心选一选
-
1. 9的相反数是（ ）A、﹣9 B、9 C、±9 D、2. 下列各式计算正确的是（ ）A、a2+2a3=3a5 B、（2b2）3=6b5 C、（3xy）2÷（xy）=3xy D、2x•3x5=6x63. 下列几何体中，俯视图相同的是（ ）
A、①② B、①③ C、②③ D、②④4. 下列图形中，既是轴对称图形，又是中心对称图形的是（ ）A、
B、
C、
D、
5.如图，一次函数y=（m﹣2）x﹣1的图象经过二、三、四象限，则m的取值范围是（ ）
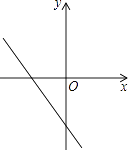A、m＞0 B、m＜0 C、m＞2 D、m＜26. 某校在“校园十佳歌手”比赛上，六位评委给1号选手的评分如下：90，96，91，96，95，94．那么，这组数据的众数和中位数分别是（ ）A、96，94.5 B、96，95 C、95，94.5 D、95，957. 如图，PA、PB分别切⊙O于A、B两点，点C在优弧 上，∠P=80°，则∠C的度数为（ ）
A、50° B、60° C、70° D、80°8. 如图，菱形纸片ABCD中，∠A=60°，折叠菱形纸片ABCD，使点C落在DP（P为AB中点）所在的直线上，得到经过点D的折痕DE．则∠DEC的大小为（ ）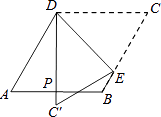
A、78° B、75° C、60° D、45°9. 在下列命题中，正确的是（ ）A、一组对边平行的四边形是平行四边形 B、有一个角是直角的四边形是矩形 C、有一组邻边相等的平行四边形是菱形 D、对角线互相垂直平分的四边形是正方形二、细心填一填
-
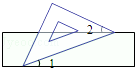
10. 科学家测量到某种细菌的直径为0.00001917mm，将这个数据用科学记数法表示为 ．11. 如图，把一块含有45°角的直角三角板的两个顶点放在直尺的对边上．如果∠1=20°，那么∠2的度数是 ．
12. 从大小形状完全相同标有1、2、3数字的三张卡片中随机抽取两张，和为偶数的概率为 ．13. 若一圆锥的轴截面是等边三角形，则其侧面展开图的圆心角是 ．14. 如图，在等边△ABC中，点D、E分别在BC、AC边上，且∠ADE=60°，AB=3，BD=1，则EC= ．
15. 如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y= x2+k与扇形OAB的边界总有两个公共点，则实数k的取值范围是 ．
三、耐心做一做
-
16. 计算： ．17. 解不等式组 ，并将不等式组的解集在数轴上表示出来．18. 如图，在△ABC中，BC的垂直平分线交BC于点D，交AB延长线于点E，连接CE．求证：∠BCE=∠A+∠ACB．
19. 甲、乙两名队员参加射击训练，成绩分别被制成下列两个统计图：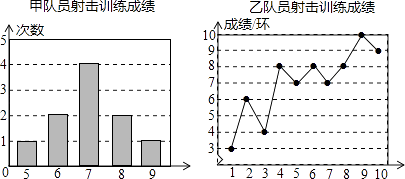
根据以上信息，整理分析数据如下：
平均成绩/环
中位数/环
众数/环
方差
甲
a
7
7
1.2
乙
7
b
8
c
(1)、写出表格中a，b，c的值；(2)、分别运用表中的四个统计量，简要分析这两名队员的射击训练成绩．若选派其中一名参赛，你认为应选哪名队员？20. 在⊙O中，AB是直径，AC是切线且AC=AB，联结BC交⊙O于点D，试仅用无刻度直尺，作以D为切点的⊙O的切线DT．
21. 小明在某一次实验中，测得两个变量之间的关系如下表所示：x
1
2
3
4
12
y
12.03
5.98
3.03
1.99
1.00
请你根据表格回答下列问题：
①这两个变量之间可能是怎样的函数关系？你是怎样作出判断的？请你简要说明理由；
②请你写出这个函数的解析式；
③表格中空缺的数值可能是多少？请你给出合理的数值．
22. 如图，AB为⊙O的直径，C为⊙O上一点，过点C作⊙O的切线，交BA的延长线交于点D，过点B作BE⊥BA，交DC延长线于点E，连接OE，交⊙O于点F，交BC于点H，连接AC．
(1)、求证：∠ECB=∠EBC；(2)、连接BF，CF，若CF=6，sin∠FCB= ，求AC的长．23.在矩形ABCD中，AB=4，AD=6，M是AD边的中点，P是射线AB上的一个动点（不与A，B重合），MN⊥PM交射线BC于N点．
(1)、如图1，当点N与点C重合时，求AP的长；
(2)、如图2，在点N的运动过程中，求证： 为定值；
(3)、在射线AB上，是否存在点P，使得△DCN∽△PMN？若存在，求此时AP的长；若不存在，请说明理由．24. 定义：若某抛物线上有两点A、B关于原点对称，则称该抛物线为“完美抛物线”．已知二次函数y=ax2﹣2mx+c（a，m，c均为常数且ac≠0）是“完美抛物线”：(1)、试判断ac的符号；(2)、若c=﹣1，该二次函数图象与y轴交于点C，且S△ABC=1．①求a的值；
②当该二次函数图象与端点为M（﹣1，1）、N（3，4）的线段有且只有一个交点时，求m的取值范围．