2017年福建省龙岩市中考数学一模试卷

试卷更新日期：2017-07-24 类型：中考模拟

进入出卷网下载

一、选择题

1. 3x²可以表示为（）

A、x²+x²+x² B、x²•x²•x² C、3x•3x D、9x

查看试题解析
2. 已知圆周率π=3.1415926…，将π精确到千分位的结果是（）

A、3.1 B、3.14 C、3.141 D、3.142

查看试题解析
3. 下列计算正确的是（）

A、（x+y）²=x²+y² B、（x﹣y）²=x²﹣2xy﹣y² C、（x+1）（x﹣1）=x²﹣1 D、（x﹣1）²=x²﹣1

查看试题解析
4. 如图，在△ABC中，分别以点A，B为圆心，大于 $\frac{1}{2}$ AB长为半径画弧，两弧分别交于点D，E，则直线DE是（）

A、∠A的平分线 B、AC边的中线 C、BC边的高线 D、AB边的垂直平分线

查看试题解析
5. 如图，OP是∠AOB的平分线，点P到OA的距离为3，点N是OB上的任意一点，则线段PN的取值范围为（）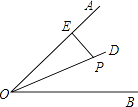

A、PN＜3 B、PN＞3 C、PN≥3 D、PN≤3

查看试题解析
6. 某电脑公司销售部为了定制下个月的销售计划，对20位销售员本月的销售量进行了统计，绘制成如图所示的统计图，则这20位销售人员本月销售量的平均数、中位数、众数分别是（）

A、19，20，14 B、19，20，20 C、18.4，20，20 D、18.4，25，20

查看试题解析
7. 已知A（2，y₁），B（﹣3，y₂），C（﹣5，y₃）三个点都在反比例函数y=﹣ $\frac{7}{x}$ 的图象上，比较y₁ ， y₂ ， y₃的大小，则下列各式正确的是（）

A、y₁＜y₂＜y₃ B、y₁＜y₃＜y₂ C、y₂＜y₃＜y₁ D、y₃＜y₂＜y₁

查看试题解析
8. 如图，在正方体的平面展开图中A、B两点间的距离为6，折成正方体后A、B两点是正方体的顶点，则这两个顶点的距离是（）

A、3 $\sqrt{2}$ B、 $\frac{3 \sqrt{2}}{2}$ C、6 D、3

查看试题解析
9. 若关于x的不等式组 ${\begin{matrix} x < 2 \\ x - a \geq 0 \end{matrix}$ 的整数解共有5个，则a的取值范围是（）

A、﹣4＜a≤﹣3 B、﹣4≤a＜﹣3 C、﹣4≤a≤﹣3 D、﹣4＜a＜﹣3

查看试题解析
10. 如图，边长为a的正方形木块在水平地面上沿直线滚动一周（没有滑动），则它的中心点O所经过的路径长为（）

A、4a B、2 $\sqrt{2}$ πa C、 $\sqrt{2}$ πa D、 $\sqrt{2}$ a

查看试题解析

二、填空题

11. 在一个不透明的口袋中装有5个红球和3个白球，他们除颜色外其他完全相同，任意摸出一个球是白球的概率为．

查看试题解析
12. 已知a=2 $\sqrt{3}$ ，b=3 $\sqrt{2}$ ，则a与b的大小关系为ab．

查看试题解析
13. 一组数：2，1，3，x，7，﹣9，…，满足“从第三个数起，前两个数依次为a、b，紧随其后的数就是2a﹣b”，例如这组数中的第三个数“3”是由“2×2﹣1”得到的，那么这组数中x表示的数为．

查看试题解析
14. 如图，在Rt△ABC中，∠C=90°，AC=4，将△ABC沿CB方向平移得到△DEF，若四边形ABED的面积等于8，则平移的距离为．

查看试题解析
15. 如图，P是抛物线y=﹣x²+x+2在第一象限上的点，过点P分别向x轴和y轴引垂线，垂足分别为A，B，则四边形OAPB周长的最大值为．

查看试题解析
16. 如图，△OAC和△BAD都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y= $\frac{k}{x}$ 在第一象限的图象经过点B，若OA²﹣AB²=8，则k的值为．

查看试题解析

三、解答题

17. 计算： $\sqrt{8}$ ﹣4sin45°+（ $\sqrt{3}$ ﹣ $\sqrt{2}$ ）⁰+2^﹣² ．

查看试题解析
18. 先化简，再求值： $\frac{1}{4}$ （4a²﹣2a﹣8）﹣（ $\frac{1}{2}$ a﹣1），其中a=1．

查看试题解析
19. 解下列方程：

(1)、x²+2x=0；

(2)、 $\frac{2}{x - 1}$
= $\frac{3}{2 x - 2}$ +1．

查看试题解析
20. 如图，在四边形ABCD中，AB∥CD，∠ABC=∠ADC，DE垂直于对角线AC，垂足是E，连接BE．

(1)、求证：四边形ABCD是平行四边形；

(2)、若AB=BE=2，sin∠ACD= $\frac{\sqrt{3}}{2}$ ，求四边形ABCD的面积．

查看试题解析
21. 有四张规格、质地相同的卡片，它们背面完全相同，正面图案分别是A．平行四边形，B．菱形，C．矩形，D．正方形，将这四张卡片背面朝上洗匀后．

(1)、随机抽取一张卡片图案是轴对称图形的概率是；

(2)、随机抽取两张卡片（不放回），求两张卡片卡片图案都是轴对称图形的概率，并用树状图或列表法加以说明．

查看试题解析
22. 如图，已知△ABC中，∠C=90°，AC=BC= $\sqrt{2}$ ，将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置，连接C′B．

(1)、请你在图中把图补画完整；

(2)、求C′B的长．

查看试题解析
23. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．

(1)、求每台A型电脑和B型电脑的销售利润；

(2)、该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？

查看试题解析
24. 如图1所示，在正方形ABCD中，AB=1， $\hat{A C}$ 是以点B为圆心，AB长为半径的圆的一段弧，点E是边AD上的动点（点E与点A，D不重合），过E作 $\hat{A C}$ 所在圆的切线，交边DC于点F，G为切点．

(1)、求证：EA=EG；

(2)、设AE=x，FC=y，求y关于x的函数关系式，并直接写出x的取值范围；

(3)、如图2所示，将△DEF沿直线EF翻折后得△D₁EF，连接AD₁ ， D₁D，试探索：当点E运动到何处时，△AD₁D与△ED₁F相似？请说明理由．

查看试题解析
25. 已知二次函数y=x²+bx+c（b，c为常数）．

(1)、当b=2，c=﹣3时，求二次函数图象的顶点坐标；

(2)、当c=10时，若在函数值y=1的情况下，只有一个自变量x的值与其对应，求此时二次函数的解析式；

(3)、当c=b²时，若在自变量x的值满足b≤x≤b+3的情况下，与其对应的函数值y的最小值为21，求此时二次函数的解析式．

查看试题解析