广东省深圳市龙华区2016-2017学年度下学期期末调研测试七年级数学试卷

试卷更新日期：2017-07-24 类型：期末考试

进入出卷网下载

一、选择题

1. 计算a²·a⁴的结果是（）

A、a⁶ B、2a⁶ C、a⁸ D、2a⁸

查看试题解析
2. 如果一个三角形的两边长分别为5,12,则第三边的长可以是（）

A、18 B、13 C、7 D、5

查看试题解析
3. 1张新版百元的人民币厚约为0.00009米,数据“0.00009米”用科学记数法可表示为（）

A、 9×10^-5米 B、9×10^-4米 C、0.9×10^-6米 D、90×10^-3米

查看试题解析
4. 下列汉字中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
5.
如图，已知直线a//b，∠1=50°，则∠2的度数为（）

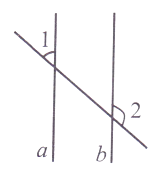A、40° B、50° C、130° D、150°

查看试题解析
6. 小亮做掷质量均匀硬币的试验,掷了10次,发现有8次正面朝上,2次正面朝下,则当他第11次掷这枚硬币时，（）

A、一定是正面朝上 B、一定是正面朝下 C、正面朝上的概率为0.8 D、正面朝上的概率为0.5

查看试题解析
7.
如图，已知AB=AD，∠BAD=∠CAE，则增加以下哪个条件仍不能判断△BAC≅△DAE的是（）

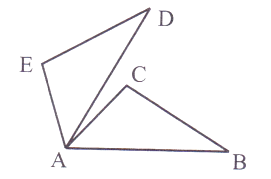A、AC=AE B、BC=DE C、∠B=∠D D、∠C=∠E

查看试题解析
8.
通过计算比较图1、图2中阴影部分的面积，正确的计算式子是（）

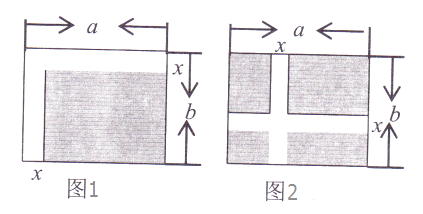A、a(b-x)=ab-ax B、b(a-x)=ab-bx C、(a-x)(b-x)=ab-ax-bx D、(a-x)(b-x)=ab-ax-bx+x²

查看试题解析
9. 下列说明中正确的是（）

A、同位角相等 B、如果一个等腰三角形的两边长分别为3和6，那么该三角形的周长为12或15 C、直线外一点与直线上各点连接的所有线段中，垂线段最短 D、事件“打开电视机，正好播放足球比赛”是必然事件

查看试题解析
10. 已知10^x=20,5^x=8，则2^x的值是（）

A、 $\frac{2}{5}$ B、 $\frac{5}{2}$ C、12 D、160

查看试题解析
11.
如图1，AB=2，P是线段AB上一点，分别以AP、BP为边作正方形.设AP=x，这两个正方形的面积之和为S，且S与x之间的关系如图2所示，则下列说明中正确的是（）

A、在点P由点A向点B运动过程中，S有最小值为2 B、在点P由点A向点B运动过程中，S的值不变 C、S与x之间的关系式为S=2x²-4 D、当0<x<1时，S的值越来越大

查看试题解析
12.
如图，△ABC中，D、E分别为AB、AC上两点，将△ABC沿直线DE折叠，使得点A落在△ABC右侧的A₁处，则∠A、∠1、∠2之间满足的关系式是（）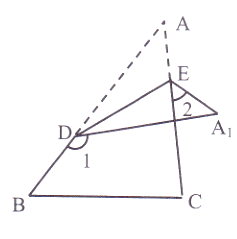

A、∠A=∠1-∠2 B、∠A= $\frac{1}{2}$ ∠1-∠2 C、∠A=∠1-2∠2 D、2∠A=∠1-∠2

查看试题解析

二、填空题

13. 计算（x+3）(x-3)的结果是.

查看试题解析
14. 有5张纸签,分别标有数字-1,0,-0.5,1,2,从中随机的抽取一张,则抽到标有的数字为正数的纸签的概率是.

查看试题解析
15. 某公交车每月的利润y(元)与乘客人数x(人)之间的关系式为y=2.5x-6000,该公交车为使每月不亏损,则每月乘客量至少需达到人.

查看试题解析
16.
如图，已知△ABC中，AB=AC，AD为高，BE为中线，AD与BE相交于点O.若BC=6，AD=7，则△AOE的面积为.

查看试题解析

三、解答题

17. 计算：

(1)、 $- 3^{2} + {(- \frac{1}{2})}^{- 2} + {(2017 - π)}^{0} - | - 2 |$

(2)、 $[5 x^{2} \cdot 2 x y^{6} + {(2 x y^{2})}^{3}] \div (4 x^{2} y^{3})$

查看试题解析
18. 先化简，再求值： $(a + 2 b) (a - b) + {(2 a - b)}^{2} - 5 a (a - b)$ ，其中a=-1，b=2.

查看试题解析
19.
填空：把下面的推理过程补充完整，并在括号内注明理由.
已知：如图，△ABC中，D、E分别为AB、AC的中点，过点C作CF//AB交DE的延长线于F.求证：AB=2CF.
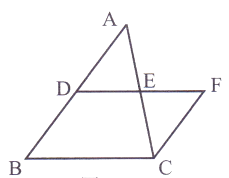
证明：∵CF//AB（已知），
∴∠ADE=∠F（ $\underline{}$ ），
∵E为AC的中点（已知），
∴AE=CE（中点的定义）.
在△ADE与△CFE中，
${\begin{cases} ∠ A D E = ∠ F \\ ___________(_____________) \\ A E = C E \end{cases}$
∴△ADE≅△CFE（ $\underline{}$ ）
∴AD=CF（ $\underline{}$ ）
∵D为AB的中点
∴AB=2AD（中点的定义）
∴AB=2CF（等量代换）

查看试题解析
20.
如图是一大一小的两个可以自由转动的转盘，甲盘被平均分成6等份，乙盘被平均分成4等份，每个转盘均被涂上红、黄、蓝三种颜色.转动转盘，当转盘停止后，指针指向的颜色即为转出的颜色.小明与小颖参与游戏：小明转动甲盘，小颖转动乙盘.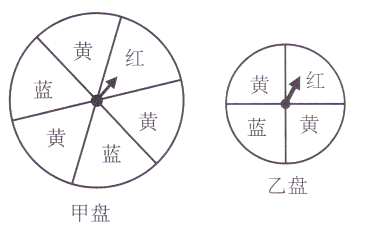

(1)、小明转出的颜色为红色的概率为；

(2)、小明转出的颜色为黄色的概率为；

(3)、小颖转出的颜色为黄色的概率为；

(4)、两人均转动转盘，如果转出的颜色为红，则胜出.你认为该游戏公平吗？为什么？

查看试题解析
21.
人的大脑所能记忆的内容是有限的，随着时间的推移，记忆的东西会逐渐遗忘.为提升记忆的效果，需要有计划的按时复习巩固.图中的实线部分是记忆保持量（%）与时间(天)之间的关系图.请根据图回答下列问题：

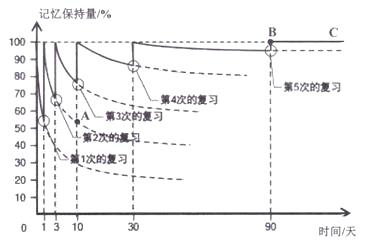(1)、图中的自变量是，因变量是；

(2)、如果不复习，3天后记忆保持量约为；

(3)、图中点A表示的意义是；

(4)、图中射线BC表示的意义是；

(5)、经过第1次复习与不进行复习，3天后记忆保持量相差约为；

(6)、10天后，经过第2次复习与从来都没有复习的记忆保持量相差约为.

查看试题解析
22. 综合题。

(1)、
如图，在△ABC中，AC=BC，∠ACB=90°，直线l过点C，分别过A、B两点作AD⊥l于点D，作BE⊥l于点E.求证：DE=AD+BE.

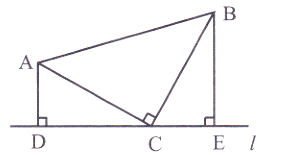(2)、
如图，已知Rt△ABC，∠C=90°.用尺规作图法作出△ABC的角平分线AD；（不写作法，保留作图痕迹）

(3)、若AB=10，CD=3，求△ABD的面积.

查看试题解析
23.
阅读下列材料，解答问题：
定义：线段AD把等腰三角形ABC分成△ABD与△ACD（如图1），如果△ABD与△ACD均为等腰三角形，那么线段AD叫做△ABC的完美分割线.

(1)、如图1，已知△ABC中，AB=AC，∠BAC=108°，AD为△ABC的完美分割线，且BD<CD，则∠B= ， ∠ADC=.

(2)、如图2，已知△ABC中，AB=AC，∠A=36°，BE为△ABC的角平分线，求证：BE为△ABC完美分割线.

(3)、如图3，已知△ABC是一等腰三角形纸片，AB=AC，AD是它的一条完美分割线，将△ABD沿直线AD折叠后，点B落在点B₁处，AB₁交CD于点E，求证：DB₁=EC.

查看试题解析