广东省东莞市四海教育集团六校联考2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期：2019-12-06 类型：期中考试
一、选择题(每题3分，共30分
-
1. 下列图形是中心对称图形，但不是轴对称图形的是（ ）A、
B、
C、
D、
2. 方程2x2=8的根为（ ）A、2 B、-2 C、±2 D、没有实数根3. 关于抛物线①y=x2：②y=-x2+1；③y=(x-2)2 ， 下列结论正确的是（ ）A、顶点相同 B、对称轴相同 C、形状相同 D、都有最高点4. 一元二次方程x2-2x-1=0的根的情况是（ ）A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断5. 下列图形绕某点旋转90°后，不能与原来图形重合的是（ ）A、
B、
C、
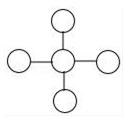D、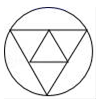
6. 若关于x的方程x2+4x+m=0有实数根，则m的取值范围是（ ）A、m≥4 B、m≤4 C、m<-4 D、m<47. 已知x1、x2、是一元二次方程x2+x-2=0的两个根，则x1+x2+x1x2的值为（ ）A、1 B、-3 C、3 D、-28. 如图，将△ABC绕顶点C旋转得到△A′B′C，且点B刚好落在A′B′上，若∠A=35°，∠BCA'=40°，则∠A′BA等于（ ）
A、30° B、35° C、40° D、45°9. 二次函数y=2x2-3的图象是一条抛物线，下列说法正确的是（ ）A、抛物线开口向下 B、抛物线经过点（2，3） C、抛物线的对称轴是直线x=1 D、抛物线与x轴有两个交点10. 关于x的一元二次方程(a-1)x2+x+a2-1=0的一个根是0，则a的值为（ ）A、1 B、-1 C、1或-1 D、2二、填空题(每题4分，共24分)
-
11. 若点M(4，-2)关于原点对称的点N的坐标是；12. 一元二次方程3x2-6x=0的根是；13. 抛物线y=(x-2)2-3的顶点坐标为；14. 方程x2-2ax+3=0有一个根是1，a的值是。15. 抛物线y=-x2+2x-3的对称轴是；16. 如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB'C'的位置，使得CC'∥AB，则∠BAB'=。
三、解答题(每题6分，共18分)
-
17. 解方程：x2+x-6=018. 如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A(-3，5)，B(-2，1)，C(-1，3)，若△ABC和△A1B1C1关于原点0成中心对称图形，画出图形并写出△A1B1C1的各顶点的坐标；
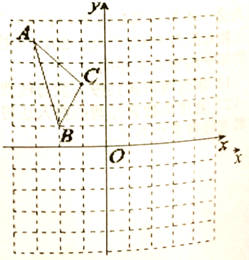19. 已知抛物线y=-x2+bx+c过点(4，0)，点(1，3)，求此抛物线的解析式。四、解答题(每题7分，共21分)
-
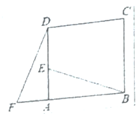
20. 已知点P(2x，y2+4)与Q(x2+1，-4y)关于原点对称，求x+y的值。21. 如图，某中学准备在校园里利用围墙的一段，再砌三面墙，围成一个矩形花园ABCD(围墙MN最长可利用25m)，现在已备足可以砌50m长的墙的材料，当矩形花园的面积为300m2时，求AB的长。
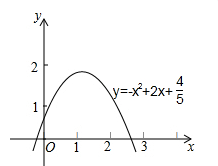
22. 根据设计图纸已知：所示直角坐标系中，水流喷出的高度y(m)与水平距离x(m)之间的函数关系式是y=-x2+2x+ ，求喷出的水流距水平面的最大高度是多少?
五、解答题(每题9分，共27分)
-
23. 为进一步发展基础教育，自2017年以来，某县加大了教育经费的投入，2017年该县投入教育经费6000万元，2019年投入教育经费8640万元，假设该县这两年投入教育经费的年平均增长率相同。(1)、求这两年该县投入教育经费的年平均增长率；(2)、若该县教育经费的投入还将保持相同的年平均增长率，请你预算2020年该县投教育经费多少万元。
