河北省衡水市景县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-06 类型：期中考试
一、选择题(本大题共14个小题。每小题3分，共42分。在每小题给出的四个选项中。只有一项是符合题目要求的)
-
1. 下列图形具有稳定性的是（ ）A、
B、
C、
D、
2. 三角形一边上的中线把原三角形分成两个（ ）A、形状相同的三角形 B、面积相等的三角形 C、直角三角形 D、周长相等的三角形3. 下列图标，是轴对称图形的是（ ）
A、
B、
C、
D、
4. 已知点A(-1，-4)，B(-1，4)，则（ ）A、A、B关于x轴对称 B、A、B关于y轴对称 C、直线AB平行于x轴 D、直线AB垂直于y轴5. 下列图形中与最右边图形全等的是（ ）
A、
B、
C、
D、
6. 三角形按边分类可以用集合来表示，如图所示，图中小椭圆圈里的A表示（ ）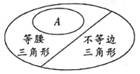
A、直角三角形 B、锐角三角形 C、钝角三角形 D、等边三角形7. 如图，两个三角形是全等三角形，x的值是（ ）
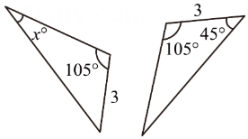A、30 B、45 C、50 D、858. 如图，线段AB与A'B' (AB=A'B')不关于直线l成轴对称的是（ ）A、
B、
C、
D、
9. 如左下图，观察图中的尺规作图痕迹，下列说法错误的是（ ）
A、AE∥BC B、∠C=∠EAC C、∠DAE=∠EAC D、∠DAE=∠B10. 右上图中的小正方形边长都相等，若△MNP≌△MEQ，则点Q可能是图中的（ ）
A、点A B、点B C、点C D、点D11. 如图，BE、CF都是△ABC的角平分线，且∠BDC=130°，则∠A=（ ）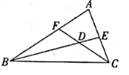
A、50° B、60° C、70° D、80°12. 一辆模型赛车，先前进1m，然后沿原地逆时针方向旋转，旋转角为a(0<a<90°)，被称为一次操作，若五次操作后，发现赛车回到出发点，则旋转角a为（ ）A、108° B、120° C、72 ° D、36°13. 对于△ABC嘉淇用尺规进行了如下操作如图：
；(1)分别以点B和点C为圆心，BA，CA为半径作弧，两弧相交于点D(2)作直线AD交BC边于点E根据嘉淇的操作方法，可知线段AE是（ ）
A、边BC的垂直平分线 B、△ABC的中线 C、△ABC的高线 D、△ABC的角平分线14. 如图，DE、FG分别是△ABC的AB、AC边上的垂直平分线，且∠BAC=100°，那么∠DAF的度数为（ ）
A、40° B、30° C、20° D、10°二、填空题(本题共3个小题，15题3分，16~17题每题2个空，每空2分，共11分)
-
15. 若一个等腰三角形的顶角等于40°，则它的底角等于。16. 如图，∠B=∠D=90°，根据角平分线性质填空
(1)、若∠1=∠2，则。(2)、若∠3=∠4，则。17. 定义：几个全等的正多边形依次有一边重合，排成一圈，中间可以围成一个正多边形，我们称作正多边形的环状连接。如图，我们可以看作正六边形的环状连接，中间围成一个边长相等的正六边形；
若正八边形作环状连接，中间可以围的正多边形的边数为；
若边长为1的正n边形作环状连接，中间围成的是等边三角形，则这个环状连接的外轮廓长为。
三、解答题(本大题共7个小题，满分67分，解答题应写出必要的解题步骤或文字说明)
-
18. 如图，在△ABC中，AD⊥BC，AE平分∠BAC，∠B=72°，∠C=30°．
(1)、求∠BAE的度数；(2)、求∠DAE的度数。19. 如图，五边形 ABCDE中，AE∥CD，∠A=107°，∠B=121°，求∠C的度数。
20. 用一条长18cm的铁丝围成一个等腰三角形，其中三边长分别为4cm，xcm，ycm，求x，y的值。21. 如图，在△ABC中，AB=AC，AD⊥BC于点D.
(1)、若∠C=42°，求∠BAD的度数；(2)、若点E在边AB上，EF∥AC交AD的延长线于点F.求证：AE=FE.
22. 如图，AB=AD，AC=AE，BC=DE，点E在BC上。
(1)、求证：△ABC≌△ADE；(2)、求证：∠EAC=∠DEB。
