广东省韶关市乐昌县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期:2019-12-06 类型:期中考试
一、选择题(共10小题,每小题3分,共30分)
-
1. 在△ABC,∠A=30°,∠B=60°,则∠C=( )A、30° B、45° C、60° D、90°2. 已知三角形的两边长分别是5和7,则第三边长a的取值范围是( )A、2<a<12 B、2≤a≤12 C、a>2 D、a<123. 下列长度的三条线段能组成三角形的是( )A、5,11,6 B、8,8,16 C、10,5,4 D、6,9,144. 观察下列图形,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
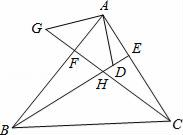
D、 5. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 如题图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定题△ABM≌△CDN的是( )
5. 如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定6. 如题图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定题△ABM≌△CDN的是( ) A、∠M=∠N B、AM∥CN C、AB=CD D、AM=CN7. 等腰三角形的一个角是70°,则它的一个底角的度数是( )A、70° B、70°或55° C、80° D、55°8. 如题图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( )
A、∠M=∠N B、AM∥CN C、AB=CD D、AM=CN7. 等腰三角形的一个角是70°,则它的一个底角的度数是( )A、70° B、70°或55° C、80° D、55°8. 如题图,△ABC与△ADC关于AC所在的直线对称,∠BCA=35°,∠B=80°,则∠DAC的度数为( ) A、55° B、65° C、75° D、85°9. 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( )
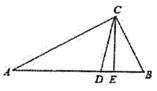
A、55° B、65° C、75° D、85°9. 如图所示为打碎的一块三角形玻璃,现在要去玻璃店配一块完全一样的玻璃,最省事的方法是( ) A、带①去 B、带②去 C、带③去 D、带①和②去10. 如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )
A、带①去 B、带②去 C、带③去 D、带①和②去10. 如图所示,在△ABC中,AC⊥BC,AE为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BD等于( )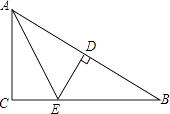 A、1cm B、2cm C、3cm D、4cm
A、1cm B、2cm C、3cm D、4cm二、填空题(共6小题,每小题4分,共24分)
-
11. 若等腰三角形的两边长为10cm、6cm,则周长为。12. 一个多边形内角和是外角和的2倍,则这个多边形的边数为。13. 已知点A(2,-3),则点A关于x轴的对称点A1的坐标是。14. 如题图,等边三角形ABC的两条角平分线BD和CD交于点D,则∠BDC等于。
 15. 如题图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是。
15. 如题图,为了使一扇旧木门不变形,木工师傅在木门的背后加钉了一根木条,这样做的道理是。 16. 如图,∠1+∠2+∠3+∠4=。
16. 如图,∠1+∠2+∠3+∠4=。
三、解答题(一)(共3题,每小题6分,共18分)
-
17. 如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D。
 18. 如图,在△ABC中,AB=AC。
18. 如图,在△ABC中,AB=AC。如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
 (1)、请画出△ABC关于y轴对称的△A1B1C1;(2)、直接写出A1 , B1 , C1的坐标。19. 如图
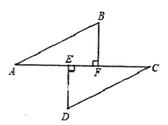
(1)、请画出△ABC关于y轴对称的△A1B1C1;(2)、直接写出A1 , B1 , C1的坐标。19. 如图已知:如图,DE⊥AC于点E,BF⊥AC于点F,CD∥AB, AB=CD。
求证:△ABF≌△CDE。
四、解答题(二)(共3题,每小题7分,共21分)
-
20. 如图
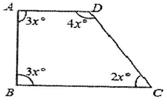 (1)、求图形中的x的值;(2)、求:∠A、∠B、∠C、∠D的度数。21. 如图:已知∠B=40°,∠C=59°,∠DEC=47°求∠F的度数。
(1)、求图形中的x的值;(2)、求:∠A、∠B、∠C、∠D的度数。21. 如图:已知∠B=40°,∠C=59°,∠DEC=47°求∠F的度数。 22. 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,若AB+BC=6,求△BEC的周长。
22. 如图,在△ABC中,AB=AC,AB的垂直平分线DE交AC于点E,若AB+BC=6,求△BEC的周长。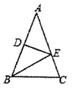
五、解答题(三)(共3题,每小题9分,共27分)
-
23. 如图①,在△ABC中,∠BAC=90°,AB=AC,直线l经过点A,且BD⊥l于点D,CE⊥l于点E
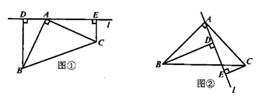 (1)、求证:BD+CE=DE(2)、当变换到如图②所示的位置时,试探究BD、CE、DE的数量关系,请说明理由。
(1)、求证:BD+CE=DE(2)、当变换到如图②所示的位置时,试探究BD、CE、DE的数量关系,请说明理由。