安徽省亳州市利辛县2019-2020学年九年级上学期数学第二次月考试卷
试卷更新日期:2019-12-06 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 若线段a=2cm,b=3cm,c=4cm,则线段a,b,c的第四比例项是( )A、 cm B、 cm C、5cm D、6cm2. 如图,点P在反比例函数y= 的图象上,过点P作PA⊥y轴于点A,若△OPA的面积为2,则k的值为( )
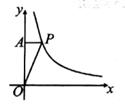 A、1 B、2 C、4 D、-43. 如图,一组平行线l1∥l2∥l3 , 与直线a相交于点A,B,C;与直线b相交于点D,E,F.若AB:BC=2:3,且DF=15,则EF=( )
A、1 B、2 C、4 D、-43. 如图,一组平行线l1∥l2∥l3 , 与直线a相交于点A,B,C;与直线b相交于点D,E,F.若AB:BC=2:3,且DF=15,则EF=( )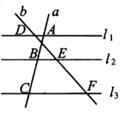 A、6 B、8 C、9 D、104. 把二次函数y=x2-4x+3配方成顶点形式y=a(x+h)2+k,结果是( )A、y=(x-2)2+1 B、y=(x-2)2-1 C、y=(x-4)2-13 D、y=(x+2)2-15. 若抛物线y=-x2+bx+c的对称轴位于直线x=-2的左侧,则下列结论正确的是( )A、b<-4 B、b<-2 C、b>-4 D、b>-26. 如图,BD是四边形ABCD的对角线,若∠ABD=∠C=90°,则添加下列条件仍不能判断△ABD∽△DCB的是( )
A、6 B、8 C、9 D、104. 把二次函数y=x2-4x+3配方成顶点形式y=a(x+h)2+k,结果是( )A、y=(x-2)2+1 B、y=(x-2)2-1 C、y=(x-4)2-13 D、y=(x+2)2-15. 若抛物线y=-x2+bx+c的对称轴位于直线x=-2的左侧,则下列结论正确的是( )A、b<-4 B、b<-2 C、b>-4 D、b>-26. 如图,BD是四边形ABCD的对角线,若∠ABD=∠C=90°,则添加下列条件仍不能判断△ABD∽△DCB的是( )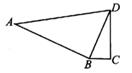 A、AD∥BC B、AD⊥CD C、BD2=AD·BC D、BD平分∠ADC7. 在压力一定的情况下,压强p(pa)与接触面积S(m2)成反比例,某木块竖直放置与地面的接触面积S=0.3m2时,P=20000pn,若把木块横放,其与地面的接触面积为2m2 , 则它能承受的压强为( )A、1000pa B、2000pa C、3000pa D、4000pa8. 如图,△ABC中,AB=AC=10,点D在BC上,连接AD,若CD=AB,AD=BD,则BC的长为( )
A、AD∥BC B、AD⊥CD C、BD2=AD·BC D、BD平分∠ADC7. 在压力一定的情况下,压强p(pa)与接触面积S(m2)成反比例,某木块竖直放置与地面的接触面积S=0.3m2时,P=20000pn,若把木块横放,其与地面的接触面积为2m2 , 则它能承受的压强为( )A、1000pa B、2000pa C、3000pa D、4000pa8. 如图,△ABC中,AB=AC=10,点D在BC上,连接AD,若CD=AB,AD=BD,则BC的长为( ) A、-5+5 B、5+5 C、10+5 D、15-59. 已知,二次函数y=ax2+bx+c(a≠0),下表列出了该函数的x,y的部分对应值:
A、-5+5 B、5+5 C、10+5 D、15-59. 已知,二次函数y=ax2+bx+c(a≠0),下表列出了该函数的x,y的部分对应值:x
…
-2
-1
0
1
2
3
…
y
…
4
5
4
1
-4
-11
请根据表中信息回答问题:一元二次方程ax2+bx+c+11=0的解是( )
A、x1=2,x2=-3 B、x1=-5,x2=-3 C、x1=-4,x2=3 D、x1=-5,x2=310. 已知:如图,菱形ABCD的周长为20cm,对角线AC=8cm,直线l从点A出发,以1cm/s的速度沿AC向右运动,直到过点C为止在运动过程中,直线l始终垂直于AC,若平移过程中直线l扫过的面积为S(cm2),直线l的运动时间为t(s),则下列最能反映S与t之间函数关系的图象是( )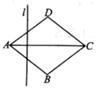 A、
A、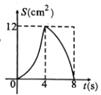 B、
B、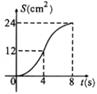 C、
C、 D、
D、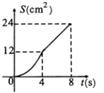
二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若 ,则 =。12. 已知点A(-2,y1)和B(1,y2)都在反比例函数y= 的图象上,则y1y2(填”>”或”=”或“<”)13. 某校九年级数学兴趣小组经过市场调查,整理出某种商品在第x天(1≤x≤40,且x为正整数)的售价与销量的相关信息如下表:
时间(天)
1≤x≤40
售价(元/件)
x+35
每天销量(件)
150-2x
已知该商品的进价为每件30元,设销售该商品的每天利润为w元.则w与x的函数表达式为。
14. 如图,矩形ABCD中,AB=3,BC=4,点P是对角线AC上一动点,过点P作PE⊥AD于点E,若点P,A,B构成以AB为腰的等腰三角形时,则线段PE的长是。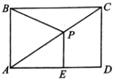
三、(本大题共2小题,每小题8分,满分16分)
-
15. 已知 ,求 的值。16. 已知二次函数y=x2-bx+c的图象经过点(-2,3)和(1,6),试确定二次函数的表达式。
四、(本大题共2小题,每小题8分,满分16分)
-
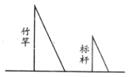
17. 《孙子算经》是中国古代重要的数学著作,成书于约一千五百年前.其中有首歌谣:今有竿不知其长,量得影长一丈五尺.立一标杆,长一尺五寸,影长五寸,问竿长几何?
意即:有一根竹竿不知道有多长,量出它在太阳下的影子长一丈五尺.同时立一根一尺五寸的小标杆,它的影长五寸(提示:1丈=10尺,1尺=10寸),求竹竿的长。
 18. 在10×10网格中建立如图所示的平面直角坐标系,△ABC是格点三角形(顶点是网格线的交点)
18. 在10×10网格中建立如图所示的平面直角坐标系,△ABC是格点三角形(顶点是网格线的交点)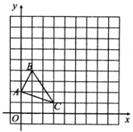 (1)、以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A1B1C1;(2)、△A1B1C1的面积是。
(1)、以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形△A1B1C1;(2)、△A1B1C1的面积是。五、(本大题共2小题,每小题10分,满分20分)
-
19. 【操作、填空】如图, ABCD中,对角线AC=a,点E是边AB上一动点,连接DE交AC于点M。
 (1)、若AE=BE,则AM的长为;(用含a的式子表示,下同)(2)、若AE=2BE,则AM的长为;(3)、若AE=3BE,则AM的长为;20. 如图是一个三角形余料示意图,它三边长分别为AC=30cm,BC=40cm,AB=50cm,现要把它加工成正方形零件,使正方形的一边DE位于边AB上,另外两个顶点F,G分别在边AC,BC上。求这个正方形零件DEFG的边长。
(1)、若AE=BE,则AM的长为;(用含a的式子表示,下同)(2)、若AE=2BE,则AM的长为;(3)、若AE=3BE,则AM的长为;20. 如图是一个三角形余料示意图,它三边长分别为AC=30cm,BC=40cm,AB=50cm,现要把它加工成正方形零件,使正方形的一边DE位于边AB上,另外两个顶点F,G分别在边AC,BC上。求这个正方形零件DEFG的边长。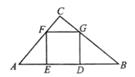
六、(本大题满分12分)
-
21. 如图,在平面直角坐标系中,一次函数y=-3x+6的图象与x轴、y轴分别交于A、B两点,以AB为边长在第一象限内作正方形ABCD,若反比例函数y= (k≠0)的图象经过顶点D。
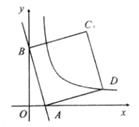 (1)、试确定k的值;(2)、若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数y= 的图象上,试确定n的值。
(1)、试确定k的值;(2)、若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数y= 的图象上,试确定n的值。七、(本大题满分12分)
-
22. 如图1,△ABC中,AB=AC,点D在边BC上,点E在边AC上,且∠ADE=∠B。
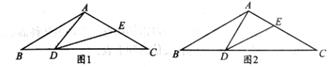 (1)、求证:△ABD∽△DCE;(2)、若AB=10,BC=16,DE∥AB,如图2,求BD的长
(1)、求证:△ABD∽△DCE;(2)、若AB=10,BC=16,DE∥AB,如图2,求BD的长八、(本大题满分14分)
-
23. 已知抛物线y=2x2+8x+6与x轴交于点A,B(点A在点B的左侧),与y轴交于点C。
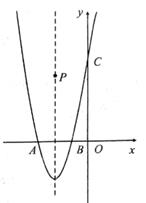 (1)、求点A,点C的坐标;(2)、我们规定:对于直线l1:y=k1x+b1 , 直线l2:y=k2x+b2 , 若k1:k2=-1,则直线l1⊥l2;反过来也成立。请根据这个规定解决下列问题:
(1)、求点A,点C的坐标;(2)、我们规定:对于直线l1:y=k1x+b1 , 直线l2:y=k2x+b2 , 若k1:k2=-1,则直线l1⊥l2;反过来也成立。请根据这个规定解决下列问题:①直线3x+2y=1与直线x-3y=4是否垂直?并说明理由;
②若点P是抛物线y=2x2+8x+6的对称轴上一动点,是否存在点P与点A,点C构成以AC为直角边的直角三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
-
-