江苏省宿迁市沭阳县2019-2020学年高一上学期数学期中考试试卷

试卷更新日期：2019-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 设集合 $U = {- 1, 0, 1, 2, 4}$ ，集合 $C_{U} M = {- 1, 1}$ ，则集合 $M =$ （）

A、 ${0, 2}$ B、 ${0, 4}$ C、 ${2, 4}$ D、 ${0, 2, 4}$

查看试题解析
2. 函数y= ${log}_{\frac{1}{2}} (2 x - 1)$ 的定义域为（）

A、（ $\frac{1}{2}$ ，+∞） B、［1，+∞ $)$ C、（ $\frac{1}{2}$ ，1 $]$ D、（－∞，1）

查看试题解析
3. 已知集合 $A = [1 ， 4) ， B = (- \infty ， a)$ ，若 $A \subseteq B$ ，则实数 $a$ 的取值范围为（）

A、 $a > 4$ B、 $a \leq 1$ C、 $a \geq 4$ D、 $a < 1$

查看试题解析
4. 下列每组函数是同一函数的是（）

A、f(x)=x-1, $g (x) = {(\sqrt{x - 1})}^{2}$ B、f(x)=|x-3|, $g (x) = \sqrt{{(x - 3)}^{2}}$ C、 $f (x) = \frac{x^{2} - 4}{x - 2}$ ,g(x)=x+2 D、 $f (x) = \sqrt{(x - 1) (x - 3)}$ , $g (x) = \sqrt{x - 1} \cdot \sqrt{x - 3}$

查看试题解析
5. 若 $a = {0.3}^{2}, b = {log}_{2} 0.3, c = 2^{0.3}$ ，则 $a, b, c$ 的大小关系是（）

A、 $a < c < b$ B、 $a < b < c$ C、 $b < a < c$ D、 $b < c < a$

查看试题解析
6. 函数 $f (x) = \frac{1}{x} - 2 x$ 在区间 $[- 2, - \frac{1}{2}]$ 上的最小值为（）

A、1 B、 $\frac{7}{2}$ C、 $- \frac{7}{2}$ D、 $- 1$

查看试题解析
7. 集合 $A = {x||x-a|<1,x \in R}, B = {x | 1 < x < 5, x \in R} . 若 A \cap B = \emptyset ，$ 则实数a的取值范围是（）

A、 ${a | 0 \leq a \leq 6}$ B、 ${a | a \leq 2 或 a \geq 4}$ C、 ${a | a \leq 0 或 a \geq 6}$ D、 ${a | 2 \leq a \leq 4}$

查看试题解析
8. 方程 $x^{\frac{1}{3}} - {(\frac{1}{2})}^{x - 2} = 0$ 的解所在的区间为（）

A、 $(0, 1)$ B、 $(1, 2)$ C、 $(2, 3)$ D、 $(3, 4)$

查看试题解析
9. 下列函数是偶函数且在 $(- \infty, 0)$ 上是减函数的是（）

A、 $y = x + 1$ B、 $y = \frac{x}{x^{2} - 1}$ C、 $y = x^{2} - 1$ D、 $y = x + \frac{3}{4}$

查看试题解析
10. 已知 $f (x) = {\begin{array}{l} x - 10 (x \geq 3) \\ f (x + 2) (x < 3) \end{array}$ ，则 $f (2)$ 的值为（）

A、8 B、 $- 8$ C、6 D、 $- 6$

查看试题解析
11. 函数 $y = \frac{e^{x} + e^{- x}}{e^{x} - e^{- x}}$ 的图像大致为（）

A、 B、 C、 D、

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} (2 a - 1) x, (x > 1) \\ \log_{a} x - \frac{1}{3}, (0 < x \leq 1) \end{array}$ ，当 $x_{1} > 0, x_{2} > 0$ 且 $x_{1} \neq x_{2}$ 时， $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ ，则实数 $a$ 的取值范围是（）

A、 $(0, \frac{1}{2})$ B、 $[\frac{1}{3}, \frac{1}{2})$ C、 $(0, \frac{1}{3}]$ D、 $(- \infty, \frac{1}{3}]$

查看试题解析

二、填空题

13. 已知幂函数f（x）=x^α的图象过点（ $\frac{1}{2}$ ， $\frac{\sqrt{2}}{2}$ ），则α= ．

查看试题解析
14. 某工厂生产某种产品的月产量与月份之间满足关系 .现已知该厂今年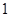月份、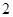月份生产该产品分别为万件、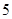万件．则此工厂月份该产品的产量为万件．

查看试题解析
15. 函数y＝log₃（﹣x²+x+6）的单调递减区间是．

查看试题解析
16. 已知函数 $f (x) = | x | - x + 1$ ，则不等式 $f (1 - x^{2}) > f (1 - 2 x)$ 的解集为．

查看试题解析

三、解答题

17. 已知全集U={x|x≤4}，集合A={x|﹣2<x<3}，B={x|﹣3≤x≤2}.

(1)、求A∩B；

(2)、求(∁_UA)∪B；

查看试题解析
18. 求值：

(1)、 ${(\lg 2)}^{2} + \lg 5 \lg 20$ ；

(2)、 ${(2 \frac{1}{4})}^{\frac{1}{2}} - {(- 9.6)}^{0} - {(3 \frac{3}{8})}^{- \frac{2}{3}} + {(1.5)}^{- 2}$ .

查看试题解析
19. 已知 $f (x) = \log_{2} \frac{1 + x}{1 - x}$ ．

(1)、求 $f (x)$ 的定义域；

(2)、判断 $f (x)$ 的奇偶性并给予证明．

查看试题解析
20. 甲厂根据以往的生产销售经验得到下面有关生产销售的统计规律：每生产产品 $x$ （百台），其总成本为 $G (x)$ （万元），其中固定成本为2.8万元，并且每生产1百台的生产成本为1万元（总成本=固定成本+生产成本），销售收入 $R (x)$ （万元）满足 $R (x) = {\begin{array}{l} - 0.4 x^{2} + 3.4 x + 0.8 (0 \leq x \leq 5) \\ 9 (x > 5) \end{array}$ ，假定该产品产销平衡（即生产的产品都能卖掉），根据上述统计规律，完成下列问题：

(1)、写出利润函数 $y = f (x)$ 的解析式（利润=销售收入－总成本）；

(2)、甲厂生产多少台产品时，可使盈利最多？

查看试题解析
21. 已知函数 $f (x) = \frac{3 x + 7}{x + 2} .$

(1)、判断并证明函数 $f (x)$ 在 $(- 2, + \infty)$ 的单调性；

(2)、若函数 $f (x)$ 的定义域为 $(- 2, 2)$ 且满足 $f (- 2 m + 3) > f (m^{_{2}})$ ，求 $m$ 的范围.

查看试题解析
22. 已知 $x = 1$ 是函数 $(x) (x) = a x^{2} - 2 a x + 1$ 的零点， $f (x) = \frac{g (x)}{x}$ .

(1)、求实数 $a$ 的值；

(2)、若不等式 $f (\ln x) - k \ln x \geq 0$ 在 $x \in [e, e^{2}]$ 上恒成立，求实数 $k$ 的取值范围；

(3)、若方程 $f (| 2^{x} - 1 |) + k (\frac{3}{| 2^{x} - 1 |}) - 3 k = 0$ 有三个不同的实数解，求实数 $k$ 的取值范围.

查看试题解析