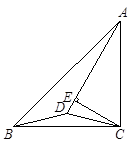河北省保定市定州市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-06 类型：期中考试
一、单选题
-
1. 下列图形中，为轴对称图形的是（ ）A、
B、
C、
D、
2. 以下各组线段为边，能组成三角形的是（ ）A、2，4，6 B、8，6，4 C、2，3，6 D、6，7，143. 如图，点A的坐标（﹣1，2），点A关于y轴的对称点的坐标为（ ）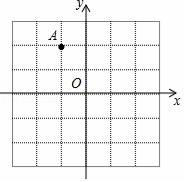
A、（1，2） B、（﹣1，﹣2） C、（1，﹣2） D、（2，﹣1）4. 如图，过△ABC的顶点A，作BC边上的高，以下作法正确的是（ ）A、
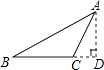B、
C、
D、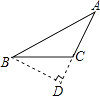
5. 在△ABC中，∠A：∠B：∠C＝2：2：5，则△ABC是（ ）A、等腰三角形 B、等边三角形 C、直角三角形 D、锐角三角形6. 若多边形的每一个内角都等于150o ， 则从此多边形的一个顶点出发的对角钱有（ ）A、10条 B、9条 C、8条 D、7条7. 如图，点D，E分别在线段AB，AC上，CD与BE相交于O点，已知AB=AC，现添加以下的哪个条件仍不能判定△ABE≌△ACD（ ）
A、∠B=∠C B、AD=AE C、BD=CE D、BE=CD8. 如图，∠B=∠D=90°，CB=CD，∠1=30°，则∠2=（ ）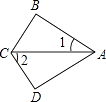
A、30° B、40° C、50° D、60°9. 如图所示，一个直角三角形纸片，剪去这个直角后，得到一个四边形，则∠1+∠2的度数为（ ）
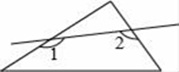A、150° B、180° C、240° D、270°10. 如图，AB＝AC，∠BAC＝100°，AB的垂直平分线交BC于点D，那么∠DAC的度数为（ ）
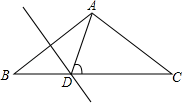A、80° B、70° C、60° D、50°11. 如图，BD是△ABC的角平分线，DE∥BC，DE交AB于E，若AB＝BC，则下列结论中错误的是（ ）
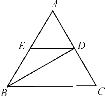A、BD⊥AC B、∠A＝∠EDA C、2AD＝BC D、BE＝ED12. 如图，在 中， ，BC边上的高 ，E是AD上的一个动点，F是边AB的中点，则 的最小值是（ ）
A、5 B、6 C、7 D、8二、填空题
-
13. 等腰三角形的顶角是50°，则它一腰上的高与底边的夹角为.14. 等腰三角形的周长为20cm，且一边长为6cm，则它的腰长为.15. 如图所示，∠A+∠B+∠C+∠D+∠E= ．
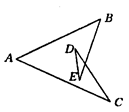16. 如图，在△ABC中，AB=AC，∠B=30°，AB的垂直平分线EF交AB于点E，交BC于点F，EF=2，则BC的长为.
17. 如图，在Rt△ABC中，∠C＝90°，AD平分∠BAC，交BC于点D，且DA＝DB．若CD＝3，则BC＝ ．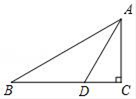
18. 已知一张三角形纸片 如图甲 ，其中 将纸片沿过点B的直线折叠，使点C落到AB边上的E点处，折痕为 如图乙 再将纸片沿过点E的直线折叠，点A恰好与点D重合，折痕为 如图丙 原三角形纸片ABC中， 的大小为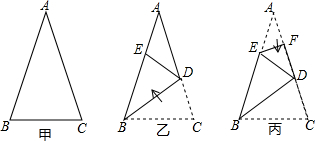
三、解答题
-
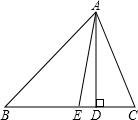
19. 已知：如图，△ABC中，AD是高，AE平分∠BAC，∠B＝50°，∠C＝80°.求∠DAE的度数.
20. 如图，已知∠ACB＝90°，点D是AB上一点，若DB＝DC．求证：点D是AB的中点.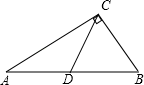
21. △ABC在平面直角坐标系中的位置如图所示，A、B、C三点在格点(小正方形的顶点)上.
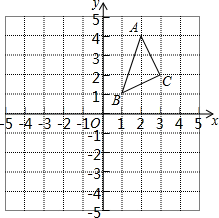(1)、作出△ABC关于x轴对称的△A1B1C1 ， 写出点A1、B1、C1的坐标；(2)、求△ABC的面积.22. 已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，求证：DE=DF．
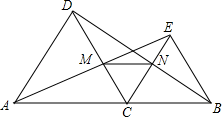
23. 如图，是由4×4个大小完在一样的小正方形组成的方格纸，其中有两个小正方形是涂黑的，请再选择三个小正方形并涂黑，使图中涂黑的部分成为轴对称图形.并画出它的一条对称轴(如图例.画对一个得1分)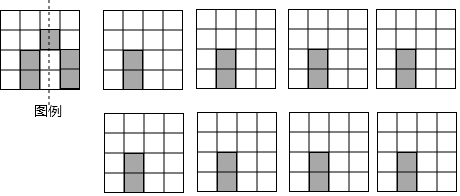
24. 如图，CN是等边△ABC的外角∠ACM内部的一条射线，点A关于CN的对称点为D，连接AD，BD，CD，其中AD，BD分别交射线CN于点E，P.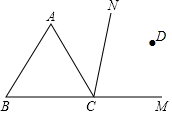
(Ⅰ)依题意补全图形.
(Ⅱ)若∠ACN＝α，求∠BDC的大小(用含α的式子表示).
(Ⅲ)若PA＝x，PC＝y，求PB的长度(用x，y的代数式表示).
