北京市五中分校2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下面有4个汽车标志图案，其中是轴对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 用科学记数法表示 $0.0002085$ 正确的是（）

A、 $2.085 \times 10^{- 3}$ B、 $2.085 \times 10^{- 4}$ C、 $2.085 \times 10^{- 5}$ D、 $2.085 \times 10^{- 6}$

查看试题解析
3. 点M（-3，-1）关于x轴的对称点N的坐标是（）

A、（3,1） B、（-3,1） C、（-3，-1） D、（3，-1）

查看试题解析
4. 下列运算正确的是（）

A、 $b^{5} \div b^{3} = b^{2}$ B、 ${(b^{5})}^{2} = b^{7}$ C、 $b^{2} \cdot b^{4} = b^{8}$ D、 $a \cdot （ a - 2 b ） = a^{2} + 2 a b$

查看试题解析
5. 计算 $3^{- 2}$ 的结果是（）

A、9 B、－9 C、 $\frac{1}{9}$ D、 $- \frac{1}{9}$

查看试题解析
6. 等腰三角形一边长等于5，一边长等于9，则它的周长是 ( ）

A、14 B、23 C、19或23 D、19

查看试题解析
7. 下列分解因式正确的是（　　）

A、x³﹣x=x（x²﹣1） B、m²+m﹣6=（m+3）（m﹣2） C、（a+4）（a﹣4）=a²﹣16 D、x²+y²=（x+y）（x﹣y）

查看试题解析
8. 下列各式中，正确的是（）．

A、 $\frac{1 + b}{a + 2 b} = \frac{1}{a + 2}$ B、 $\frac{a - 2}{a^{2} - 4} = \frac{1}{a - 2}$ C、 $\frac{a + 1}{a - 1} = \frac{a^{2} - 1}{{(a - 1)}^{2}}$ D、 $\frac{- 1 - b}{a} = - \frac{1 - b}{a}$

查看试题解析
9. 在平面直角坐标系中，点A的坐标为（1,1）在坐标轴上找到一点P使△AOP为等腰三角形，这样的点P个数为（）

A、8 个 B、7 个 C、6 个 D、5 个

查看试题解析
10. 如图，已知： $∠ M O N = 30 °$ ，点 $A_{1}$ 、 $A_{2}$ 、 $A_{3}$ …在射线 $O N$ 上，点 $B_{1}$ 、 $B_{2}$ 、 $B_{3}$ …在射线 $O M$ 上， $△ A_{1} B_{1} A_{2}$ 、 $△ A_{2} B_{2} A_{3}$ 、 $△ A_{3} B_{3} A_{4}$ …均为等边三角形，若 $O A_{1} = \frac{1}{2}$ ，则 $△ A_{6} B_{6} A_{7}$ 的边长为（）

A、6 B、12 C、16 D、32

查看试题解析

二、填空题

11. 若分式 $\frac{x^{2} - 1}{x + 1}$ 的值为0，则 $x^{2} - 2 x$ 的值为.

查看试题解析
12. ${(- 2)}^{0}$ = ．

查看试题解析
13. 已知x-y=1，则 $x^{2} - y^{2} - 2 y$ 的值为.

查看试题解析
14. 已知 $x + \frac{1}{x} = 3$ ，则代数式 $x^{2} + \frac{1}{x^{2}}$ 的值为．

查看试题解析
15. ${(- \frac{2}{3})}^{2018} \times {1.5}^{2019} \div {(- 1)}^{2020}$ =.

查看试题解析
16. 如图，在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $∠ A = 15 °$ ， $A B$ 的垂直平分线与 $A C$ 交于点 $D$ ，与 $A B$ 交于点 $E$ ，连接 $B D$ .若 $A D = 12$ ，则 $B C$ 的长为.

查看试题解析
17. 等腰三角形的一内角为80°，则一腰上的高与底边的夹角为.

查看试题解析
18. 如图，等腰三角形ABC的底边BC长为2，面积是4，腰AC的垂直平分线 EF分别交AC，AB边于E，F 点，若点D 为BC边的中点，点M 为线段EF上一动点，则△CDM 周长的最小值为。

查看试题解析

三、解答题

19. 因式分解

(1)、 $a^{3}$ −4a

(2)、2 $x^{3}$ y−20 $x^{2}$ y+50xy

查看试题解析
20. 整式计算。

(1)、 $2 {(a^{2})}^{2} - 6 a \cdot a^{3} + {(- 2 a)}^{4}$

(2)、先化简，再求值：x(x+1)−(x+2)(2−x)−2 ${(x + 2)}^{2}$ ，其中x=-1

查看试题解析
21. 分式计算：

(1)、 $\frac{3 a b + a^{2}}{a^{2} - b^{2}} \div \frac{a + 3 b}{a - b}$

(2)、 ${(- \frac{a}{b})}^{2} \cdot {(\frac{b}{a^{2}})}^{2} \div {(- 2 a b)}^{2}$

(3)、 $\frac{2}{2 a + 3} + \frac{3}{3 - 2 a} + \frac{2 a + 15}{4 a^{2} - 9}$

(4)、先化简，再求值： $(m + \frac{4 m + 4}{m}) \div \frac{m + 2}{m^{2}}$ ，其中m=1.

查看试题解析
22. 已知，如图， $E$ 是 $A C$ 上一点， $A B = C E$ ， $A B ∥ C D$ ， $A C = C D$ .求证： $B C = E D$ .

查看试题解析
23. 如图，在△ABC中，AC=AB，点D在AB上，BC=BD，∠ACD=15°.求∠B的度数.

查看试题解析
24. 在等边△ABC外作射线AD，使得AD和AC在直线AB的两侧，∠BAD=α（0°＜α＜180°），点B关于直线AD的对称点为P，连接PB，PC．

(1)、依题意补全图1；

(2)、在图1中，求△BPC的度数；

(3)、直接写出使得△PBC是等腰三角形的α的值．

查看试题解析
25. 阅读材料
小明遇到这样一个问题：求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数.

小明想通过计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得的多项式解决上面的问题，但感觉有些繁琐，他想探寻一下，是否有相对简洁的方法.

他决定从简单情况开始，先找 $(x + 2) (2 x + 3)$ 所得多项式中的一次项系数，通过观察发现：

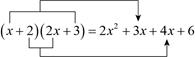
也就是说，只需用 $x + 2$ 中的一次项系数1乘以 $2 x + 3$ 中的常数项3，再用 $x + 2$ 中的常数项2乘以 $2 x + 3$ 中的一次项系数2，两个积相加 $1 \times 3 + 2 \times 2 = 7$ ，即可得到一次项系数.

延续上面的方法，求计算 $(x + 2) (2 x + 3) (3 x + 4)$ 所得多项式的一次项系数，可以先用 $x + 2$ 的一次项系数1， $2 x + 3$ 的常数项3， $3 x + 4$ 的常数项4，相乘得到12；再用 $2 x + 3$ 的一次项系数2， $x + 2$ 的常数项2， $3 x + 4$ 的常数项4，相乘得到16；然后用 $3 x + 4$ 的一次项系数3， $x + 2$ 的常数项2 $2 x + 3$ 的常数项3，相乘得到18.最后将12，16，18相加，得到的一次项系数为46.

参考小明思考问题的方法，解决下列问题：

(1)、计算 $(x + 4) (4 x + 3)$ 所得多项式的一次项系数为.

(2)、计算 $(x + 1) (3 x - 2) (2 x + 5)$ 所得多项式的一次项系数为.

(3)、若 $x^{2} - 3 x + 1$ 是 $x^{4} + a x^{2} + b x + 2$ 的一个因式，求 $a$ 、 $b$ 的值.

查看试题解析