北京市通州区2019-2020学年七年级上学期数学期中考试试卷

试卷更新日期：2019-12-06 类型：期中考试

进入出卷网下载

一、单选题

1. 下列四个数中，比-2大但比1小的数是（）

A、0 B、3 C、-2 D、-3

查看试题解析
2. 下列各数中是负数的是（）

A、 $| - 3 |$ B、﹣3 C、 $- (- 3)$ D、 $\frac{1}{3}$

查看试题解析
3. 如图，数轴的单位长度为1，如果点A和点C表示的有理数互为相反数，那么点B表示的有理数是（）

A、-3 B、-1 C、1 D、3

查看试题解析
4. 如图，数物上A，B，C三点表示的数分别为a，b，c，且AB=BC．如 $| b | < | a | < | c |$ ，那么关于原点0的位置，下列说法正确的是（）

A、在B，C之间更靠近B B、在B，C之间更靠近C C、在A，B之间更靠近B D、在A，B之间更靠近A

查看试题解析
5. 算式(-2)×(-2)×(-2)×(-2)×(-2)可表示为（）

A、(-2)×5 B、 $- 2^{5}$ C、 ${(- 2)}^{5}$ D、以上都不符合题意

查看试题解析
6. 如果某同学家电冰箱冷藏室的设定温度为6℃，且冷冻室的设定温度比冷藏室的温度低22℃，那么该同学家电水箱冷冻室的设定温度为（）

A、28℃ B、-28℃ C、16℃ D、-16℃

查看试题解析
7. 如果一个有理数的绝对值比它的相反数大，那么这个数是（）

A、正数 B、负数 C、负数和零 D、正数和零

查看试题解析
8. 点A，B在数轴上的位置如图所示，其对应的有理数分别是a和B.对于下列四个结论：① $b - a > 0$ ；② $| a | < | b |$ ；③ $a + b > 0$ ；④ $\frac{b}{a} > 0$ .其中正确的是（）

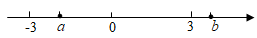A、①②③④ B、①②③ C、①③④ D、②③④

查看试题解析

二、填空题

9. 庆祝中华人民共和国成立70周年阅兵式于2019年10月1日上午在北京天安门广场隆重举行。这次阅兵编59个方(梯)队和联合军乐团，总规模约1.5万人，各型飞机160余架、装备580台(套)，是近几次阅兵中规模最大的一次，将1.5万人用科学记数法表示为人.

查看试题解析
10. 如图，数轴上点A关于原点对称的点为点B，那么点B表示的有理数的绝对值是.

查看试题解析
11. 比较大小: $- \frac{5}{7}$ $- \frac{3}{4}$ (选填“>”，“<”或“=”).

查看试题解析
12. 计算: $1 - 1 \div \frac{1}{7} \times (- 7)$ 的结果是.

查看试题解析
13. 对于一对有理数a，b，如果a≠b且a+b=0.那么这对有理数可以是a= ， b=.

查看试题解析
14. 在数轴上，点A表示的数是-3.从点A出发，沿数轴移动5个单位长度到达点B，那么点B表示的数为.

查看试题解析
15. 观察以下等式：
第1个等式： $\frac{1}{1} + \frac{0}{2} + \frac{1}{1} \times \frac{0}{2} = 1$ ；

第2个等式： $\frac{1}{2} + \frac{1}{3} + \frac{1}{2} \times \frac{1}{3} = 1$ ，

第3个等式： $\frac{1}{3} + \frac{2}{4} + \frac{1}{3} \times \frac{2}{4} = 1$ ，

第4个等式： $\frac{1}{4} + \frac{3}{5} + \frac{1}{4} \times \frac{3}{5} = 1$ ，

第5个等式： $\frac{1}{5} + \frac{4}{6} + \frac{1}{5} \times \frac{4}{6} = 1$ ，

……

按照以上规律，写出第7个等式：.

查看试题解析
16. 有理数a在数轴上的位置如图.

用“>”或”<"填空： $- \frac{1}{a}$ 0，-a+10.

查看试题解析

三、解答题

17. 在横线上直接写出下列算式的运算结果.

(1)、(+3)+(-8)=.

(2)、0-(-6)=.

(3)、 $(- \frac{1}{4}) \times (- \frac{8}{9}) =$ .

(4)、 $- 3 - | - 4 | =$ .

(5)、 $\frac{5}{2} \div (- \frac{9}{4}) =$ .

(6)、 $- 3^{2} + {(- 2)}^{2} =$ .

查看试题解析
18. 在横线上填写每步运算的依据.
解:(-6)+(-15)+(+6)

=(-6)+(+6)+(-15)()

=[(-6)+(+6)]+(-15)()

=0+(-15)()

=-15()

查看试题解析
19. 计算

(1)、(-10)-(-3)+(-5)-(+7)；

(2)、 $\frac{1}{3} - (\frac{6}{7} - \frac{8}{3}) - \frac{1}{7}$ ；

(3)、 $- 18 - 4^{2} \div (- 8) - (- 3) \times \frac{1}{9}$ ；

(4)、 $(- 5) \times (- \frac{16}{5}) + (- 7) \times \frac{16}{5} - 12 \times (- \frac{16}{5})$ .

查看试题解析

20. 科技改变世界.快递分拣机器人从微博火到了朋友圈，据介绍，这些机器人不仅可以自动规划最优路线，将包裹准确放入相应的格口，还会感应避让障碍物、自动归队取包裹，没电的时候还会自己我充电桩充电.每台分拣机器人一小时可以分拣1.8万件包襄，大大提高了分拣效率，某分栋仓库计划平均每天分栋20万件包裹，但实际每天的分拣量与计划相比会有出入，下表是该仓库10月份第三周分拣包裹的情况(超过计划量记为正，未到达计划量记为负)：

星期	一	二	三	四	五	六	七
分拣情况(单位，万件）	+6	-3	-4	+5	-1	+7	-8

(1)、该仓库本周内分拣包裹数量最多的一天是星期，最少的一天是星期，最多的一天比最少的一天多分拣万件包裹；

(2)、该仓库本周实际分拣包裹一共多少万件?

查看试题解析

21. 小华间学早晨跑步，他从自己家出发.先向东跑了2km则达小盛家，又继续向东跑了1.5km到这小昌家，然后又向西跑到学校.如果小华跑步的速度是均匀的，且到达小盛家用了8分钟，整个跑步过程共用时32分钟，以小华家为原点，向东为正方向，用1个单位长度表示1km，建立数轴.

(1)、依题意画出数轴，分别用点A表示出小盛家、用点B表示出小昌家；

(2)、在数轴上，用点C表示出学校的位置；

(3)、求小盛家与学校之间的距离.

查看试题解析
22. 如图，在数轴上有三个点A、B、C，完成系列问题：

(1)、将点B向右移动六个单位长度到点D，在数轴上表示出点D．

(2)、在数轴上找到点E，使点E到A、C两点的距离相等．并在数轴上标出点E表示的数．

(3)、在数轴上有一点F，满足点F到点A与点F到点C的距离和是9，则点F表示的数是．

查看试题解析
23. 我们新定义一种运算，用符号“⊕”表示：当 $x \leq y$ 时，x⊕y= $x^{2}$ ，当x>y时，x⊕y=y.
求算式(-4)⊕[(-2)⊕(-4)]-[(-5)⊕(-4)]的值.

查看试题解析
24. 给出如下定义：如果两个不相等的有理数a，b满足等式a-b=a
B.那么称a，b是“关联有理数对”，记作(a，b).如：因为 $3 - \frac{3}{4} = \frac{12}{4} - \frac{3}{4} = \frac{9}{4}$ ， $3 \times \frac{3}{4} = \frac{9}{4}$ .所以数对(3， $\frac{3}{4}$ )是“关联有理数对”.

(1)、在数对①(1， $\frac{1}{2}$ )、②(-1，0)、③( $\frac{5}{2}$ ， $\frac{5}{7}$ )中，是“关联有理数对”的是 (只填序号)；

(2)、若(m，n)是“关联有理数对”，则(-m，-n) “关联有理数对”(填“是”或“不是”)；

(3)、如果两个有理数是一对“关联有理数对”，其中一个有理数是5，求另一个有理数.

查看试题解析