山东省烟台市2019-2020学年高一上学期数学期中考试试卷
试卷更新日期:2019-12-06 类型:期中考试
一、单选题
-
1. 已知集合 , , ,则 ( )A、 B、 C、 D、2. 命题“ , ”的否定是( )A、 , B、 , C、 , D、 ,3. 设 ,则“ ”是“ ”的( )A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件4. 我们把含有限个元素的集合 叫做有限集,用 表示有限集合 中元素的个数.例如, ,则 .若非空集合 满足 ,且 ,则下列说法错误的是( )A、 B、 C、 D、5. 设 ,则 的最大值为( )A、 B、 C、 D、6. 下面各组函数中表示同一个函数的是( )A、 , B、 , C、 , D、 ,7. 已知 若 ,则实数 的值为( )A、 B、2 C、 D、8. 若不等式 对一切实数 都成立,则实数 的取值范围为( )A、 B、 C、 D、9. 某容器如图所示,现从容器顶部将水匀速注入其中,注满为止.记容器内水面的高度 随时间 变化的函数为 ,则 的图象可能是( )
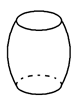 A、
A、 B、
B、 C、
C、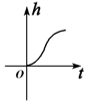 D、
D、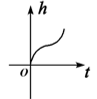 10. 已知函数 是定义在 上的单调函数, , 是其图象上的两点,则不等式 的解集为( )A、 B、 C、 D、
10. 已知函数 是定义在 上的单调函数, , 是其图象上的两点,则不等式 的解集为( )A、 B、 C、 D、二、多选题
-
11. 下列结论正确的有( )A、函数 的定义域为 B、函数 , 的图象与 轴有且只有一个交点 C、“ ”是“函数 为增函数”的充要条件 D、若奇函数 在 处有定义,则12. 十六世纪中叶,英国数学家雷科德在《砺智石》一书中首先把“ ”作为等号使用,后来英国数学家哈利奥特首次使用“ ”和“ ”符号,并逐渐被数学界接受,不等号的引入对不等式的发展影响深远.若 ,则下列命题正确的是( )A、若 且 ,则 B、若 ,则 C、若 ,则 D、若 且 ,则13. 我们把定义域为 且同时满足以下两个条件的函数 称为“ 函数”:(1)对任意的 ,总有 ;(2)若 , ,则有 成立,下列判断正确的是( )A、若 为“ 函数”,则 B、若 为“ 函数”,则 在 上为增函数 C、函数 在 上是“ 函数” D、函数 在 上是“ 函数”
三、填空题
-
14. 若函数 是定义在 上的奇函数,则 .15. 设 : , : ,若 是 的必要不充分条件,则实数 的取值范围是.16. 已知函数 与 的定义域相同,值域也相同,但不是同一个函数,则满足上述条件的一组 与 的解析式可以为.17. 定义 其中 表示 中较大的数.对 ,设 , ,函数 ,则:(1)、 ;(2)、若 ,则实数 的取值范围是.
四、解答题
-
18. 已知集合 , , .(1)、求 ;(2)、若 ,求实数 的取值范围.19. 已知函数 .(1)、求函数 的解析式;(2)、根据函数单调性的定义证明 在 上单调递减.20. 某种商品的销售价格会因诸多因素而上下浮动,经过调研得知: 年 月份第 ( , )天的单件销售价格(单位:元 ,第 天的销售量(单位:件) 为常数),且第 天该商品的销售收入为 元(销售收入 销售价格 销售量).(1)、求m的值;(2)、该月第几天的销售收入最高?最高为多少?21. 为打赢打好脱贫攻坚战,实现建档立卡贫困人员稳定增收,某地区把特色养殖确定为脱贫特色主导产业,助力乡村振兴.现计划建造一个室内面积为 平方米的矩形温室大棚,并在温室大棚内建两个大小、形状完全相同的矩形养殖池,其中沿温室大棚前、后、左、右内墙各保留 米宽的通道,两养殖池之间保留2米宽的通道.设温室的一边长度为 米,如图所示.
 (1)、将两个养殖池的总面积 表示 为的函数,并写出定义域;(2)、当温室的边长 取何值时,总面积 最大?最大值是多少?22. 已知二次函数 的图象过点 ,且不等式 的解集为 .(1)、求 的解析式;(2)、若 在区间 上有最小值 ,求实数 的值;(3)、设 ,若当 时,函数 的图象恒在 图象的上方,求实数m的取值范围.23. 经过函数性质的学习,我们知道:“函数 的图象关于 轴成轴对称图形”的充要条件是“ 为偶函数”.(1)、若 为偶函数,且当 时, ,求 的解析式,并求不等式 的解集;(2)、某数学学习小组针对上述结论进行探究,得到一个真命题:“函数 的图象关于直线 成轴对称图形”的充要条件是“ 为偶函数”.若函数 的图象关于直线 对称,且当 时, .
(1)、将两个养殖池的总面积 表示 为的函数,并写出定义域;(2)、当温室的边长 取何值时,总面积 最大?最大值是多少?22. 已知二次函数 的图象过点 ,且不等式 的解集为 .(1)、求 的解析式;(2)、若 在区间 上有最小值 ,求实数 的值;(3)、设 ,若当 时,函数 的图象恒在 图象的上方,求实数m的取值范围.23. 经过函数性质的学习,我们知道:“函数 的图象关于 轴成轴对称图形”的充要条件是“ 为偶函数”.(1)、若 为偶函数,且当 时, ,求 的解析式,并求不等式 的解集;(2)、某数学学习小组针对上述结论进行探究,得到一个真命题:“函数 的图象关于直线 成轴对称图形”的充要条件是“ 为偶函数”.若函数 的图象关于直线 对称,且当 时, .(i)求 的解析式;
(ii)求不等式 的解集.