山东省烟台市2019-2020学年高二上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 若不等式 $a x^{2} + b x + 2 > 0$ 的解集是 ${x | - \frac{1}{2} < x < \frac{1}{3}}$ ，则 $\frac{b}{a} =$ （）.

A、 $- \frac{1}{12}$ B、 $\frac{1}{12}$ C、 $- \frac{1}{6}$ D、 $\frac{1}{6}$

查看试题解析
2. 已知 $﹣ 1 < a < 0$ ， $b < 0$ ，则 $b$ ， $a b$ ， $a^{2} b$ 的大小关系是（）

A、 $b < a b < a^{2} b$ B、 $a^{2} b < a b < b$ C、 $a^{2} b < b < a b$ D、 $b < a^{2} b < a b$

查看试题解析
3. 已知数列 ${a_{n}}$ 的前n项和 $S_{n} = 3^{n} + k (k 为常数)$ ，那么下述结论正确的是（）

A、 $k$ 为任意实数时， ${a_{n}}$ 是等比数列 B、 $k$ = －1时， ${a_{n}}$ 是等比数列 C、 $k$ =0时， ${a_{n}}$ 是等比数列 D、 ${a_{n}}$ 不可能是等比数列

查看试题解析
4. 已知 $x > 1$ ，则函数 $y = x + \frac{1}{x - 1}$ 的最小值是（）

A、1 B、 $2$ C、 $3$ D、 $4$

查看试题解析
5. “中国剩余定理”又称“孙子定理”1852年英国来华传教士伟烈亚力将《孙子算经》中“物不知数问题的解法传至欧洲.1874年，英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”“中国剩余定理”讲的是一个关于整除的问题，现有这样一个整除问题：将1至2019中能被3除余1且被5除余1的数按由小到大的顺序排成一列，构成数列 ${a_{n}}$ ，则此数列的项数为（）

A、134 B、135 C、136 D、137

查看试题解析
6. 定义在 $(- 1 ， + \infty)$ 上的函数 $f (x)$ 满足 $f^{'} (x) + \cos x < 0$ ，且 $f (0) = 1$ ，则不等式 $f (x) + \sin x < 1$ 的解集为（）.

A、 $(- \infty ， 0)$ B、 $(- 1 ， 0)$ C、 $(0 ， + \infty)$ D、 $(- 1 ， 1)$

查看试题解析
7. 数列 ${\frac{1}{n (n + 2)}}$ 的前 $n$ 项和为（）.

A、 $\frac{3 n^{2} + 5 n}{4 (n + 1) (n + 2)}$ B、 $\frac{3 n^{2} + 5 n}{2 (n + 1) (n + 2)}$ C、 $\frac{n + 1}{2 (n + 2)}$ D、 $\frac{n + 1}{n + 2}$

查看试题解析
8. 在各项均为正数的等比数列 ${a_{n}}$ 中 $a_{6} = 3$ ，则 $4 a_{4} + a_{8}$ （）

A、有最小值12 B、有最大值12 C、有最大值9 D、有最小值9

查看试题解析
9. 若函数 $f (x) = x^{3} + a x - 2$ 在区间 $(1 ， + \infty)$ 内是增函数，则实数 $a$ 的取值范围是（）

A、 $(3 ， + \infty)$ B、 $[- 3 ， + \infty)$ C、 $(- 3 ， + \infty)$ D、 $(- \infty ， - 3)$

查看试题解析
10. 函数 $f (x)$ 的定义域为 $(a ， b)$ ，其导函数 $f^{'} (x)$ 在 $(a ， b)$ 的图象如图所示，则函数 $f (x)$ 在 $(a ， b)$ 内的极小值点共有（）

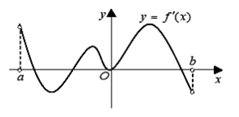A、3个 B、2个 C、1个 D、4个

查看试题解析

二、多选题

11. 下列说法正确的是（）.

A、若 $x, y > 0$ ， $x + y = 2$ ，则 $2^{x} + 2^{y}$ 的最大值为4 B、若 $x < \frac{1}{2}$ ，则函数 $y = 2 x + \frac{1}{2 x - 1}$ 的最大值为-1 C、若 $x, y > 0$ ， $x + y + x y = 3$ ，则 $x y$ 的最小值为1 D、函数 $y = \frac{1}{\sin^{2} x} + \frac{4}{\cos^{2} x}$ 的最小值为9

查看试题解析
12. 已知 ${a_{n}}$ 为等差数列，其前 $n$ 项和为 $S_{n}$ ，且 $2 a_{1} + 3 a_{3} = S_{6}$ ，则以下结论正确的是（）.

A、 $a_{10} = 0$ B、 $S_{10}$ 最小 C、 $S_{7} = S_{12}$ D、 $S_{19} = 0$

查看试题解析
13. 已知函数 $f (x) = x \ln x$ ，若 $0 < x_{1} < x_{2}$ ，则下列结论正确的是（）.

A、 $x_{2} f (x_{1}) < x_{1} f (x_{2})$ B、 $x_{1} + f (x_{1}) < x_{2} + f (x_{2})$ C、 $\frac{f (x_{1}) - f (x_{2})}{x_{1} - x_{2}} < 0$ D、当 $\ln x > - 1$ 时， $x_{1} f (x_{1}) + x_{2} f (x_{2}) > 2 x_{2} f (x_{1})$

查看试题解析

三、填空题

14. 已知 $b$ 克糖水中含有 $a$ 克糖（ $b > a > 0$ ），再添加 $m$ 克糖（ $m > 0$ ）（假设全部溶解），糖水变甜了.请将这一事实表示为一个不等式．

查看试题解析
15. 已知数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n} = 2 n^{2} + 3 n + 3$ ，则数列 ${a_{n}}$ 的通项公式为．

查看试题解析
16. 设 $f (x) = | \ln x |$ ，若函数 $g (x) = f (x) - a x$ 在区间 $(0, 4)$ 上有三个零点，则实数 $a$ 的取值范围是．

查看试题解析
17. 将边长分别为 $1 ， 2 ， 3 ， \dots ， n ， \dots (n \in N^{*})$ 的正方形叠放在一起，形成如图所示的图形，把各阴影部分所在图形的面积由小到大依次记为 $f (1) ， f (2) ， f (3) ， \dots ， f (n) ， \dots$ ，则 $f (n) =$ ，前 $n$ 个阴影部分图形的面积的平均值为．

查看试题解析

四、解答题

18. 设函数 $f (x) = \frac{a}{3} x^{3} - \frac{3}{2} x^{2} + \frac{f^{'} (1) + 4}{2} x + 1 (a \in R)$ .

(1)、若函数 $f (x)$ 在 $x = 1$ 处取得极值，求 $a$ 的值；

(2)、若不等式 $f^{'} (x) > x^{2} - x - a + 1$ 对任意 $a \in (0 ， + \infty)$ 都成立，求实数 $x$ 的取值范围.

查看试题解析
19. 已知正项等比数列 ${a_{n}}$ 是单调递增数列，且 $4 a_{3}$ 与 $3 a_{5}$ 的等差中项为 $4 a_{4}$ ， $a_{3}$ 与 $a_{7}$ 的等比中项为16.

(1)、求数列 ${a_{n}}$ 的通项公式；

(2)、令 $b_{n} = \log_{2} a_{n + 1}$ ，求数列 ${a_{n} + b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
20. 甲、乙两地相距 $120 k m$ ，汽车从甲地匀速行驶到乙地，速度不超过 $110 k m / h$ .已知汽车每小时的运输成本（以元为单位）由可变部分和固定部分组成：可变部分与速度 $v$ （单位： $k m / h$ ）的平方成正比，且比例系数为 $b$ ，固定部分为 $a$ 元.

(1)、把全程运输成本 $y$ （元）表示为速度 $v$ 的函数，并求出当 $a = 64$ ， $b = \frac{1}{144}$ 时，汽车应以多大速度行驶，才能使得全程运输成本最小；

(2)、随着汽车的折旧，运输成本会发生一些变化，那么当 $a = 100$ ， $b = \frac{1}{144}$ 元，此时汽车的速度应调整为多大，才会使得运输成本最小.

查看试题解析
21. 已知函数 $f (x) = e^{x - 1} - x$ .

(1)、求 $y = f (x)$ 在点 $(2 ， f (2))$ 处的切线方程；

(2)、若存在 $x \in [0 ， 1 + \ln \frac{4}{3}]$ ，满足 $a - e^{x - 1} + x < 0$ 成立，求实数 $a$ 的取值范围.

查看试题解析
22. 已知函数 $f (x) = \tan x - 1$ 在 $(0, + \infty)$ 上的零点按从小到大的顺序构成数列 ${a_{n}} (a \in N^{*})$ .

(1)、试判断数列 ${a_{n}}$ 是否为等差数列，并说明理由；

(2)、设 $b_{n} = \frac{4}{π} a_{n} \cdot 2^{n}$ ，求数列 ${b_{n}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
23. 已知函数 $f (x) = - x^{2} + a x - \ln x$

(1)、判断 $f (x)$ 的单调性；

(2)、若函数 $f (x)$ 存在极值，求这些极值的和的取值范围.

查看试题解析