山东省济宁市邹城市2019-2020学年高三上学期期中数学试题
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
1. 数列1, , , , ,……的一个通项公式 ( )A、 B、 C、 D、2. 设集合 , ,则 ( )A、 B、 C、 D、3. 已知向量 , ,若向量 与 垂直,则 ( )A、9 B、3 C、 D、4. 若 ,则有( )A、a<b<c B、a<c<b C、c<a<b D、b<c<a5. 在等比数列
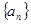 中,若 ,则 的值为( ) A、
中,若 ,则 的值为( ) A、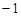 B、1
C、2
D、3
6. 如图点A为单位圆上一点, ,点A沿单位圆逆时针方向旋转角 到点B ,则 ( )
B、1
C、2
D、3
6. 如图点A为单位圆上一点, ,点A沿单位圆逆时针方向旋转角 到点B ,则 ( )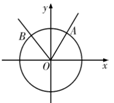 A、 B、 C、 D、7. 函数 的大致图象是( )A、
A、 B、 C、 D、7. 函数 的大致图象是( )A、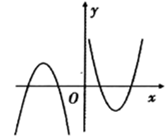 B、
B、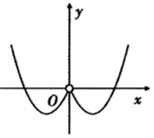 C、
C、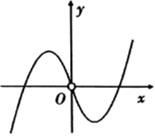 D、
D、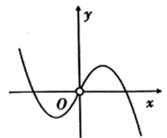 8. 已知函数 的图象与 轴的两个相邻交点的距离等于 ,若函数 的图象上各点的纵坐标不变,先将其上各点的横坐标伸长到原来的2倍,再向左平移 个单位得到函数 的图象,则函数 ( )A、 B、 C、 D、9. 设 的内角 所对的边分别为 ,且 已知 的面积 ,则 的值为( )A、 B、 C、 D、10. 关于数列 ,给出下列命题:①数列 满足 ,则数列 为公比为2的等比数列;②“ , 的等比中项为 ”是“ ”的充分不必要条件:③数列 是公比为 的等比数列,则其前 项和 ;④等比数列 的前 项和为 ,则 , , 成等比数列,其中假命题的序号是( )A、② B、②④ C、①②④ D、①③④11. 已知函数 ,若函数 ( 为常数)有三个零点,则实数 的取值范围为( )A、 B、 C、 D、12. 定义域为 的函数 图像的两个端点为 、 ,向量 , 是 图像上任意一点,其中 ,若不等式 恒成立,则称函数 在 上满足“ 范围线性近似”,其中最小正实数 称为该函数的线性近似阈值.若函数 定义在 上,则该函数的线性近似阈值是( )A、 B、 C、 D、
8. 已知函数 的图象与 轴的两个相邻交点的距离等于 ,若函数 的图象上各点的纵坐标不变,先将其上各点的横坐标伸长到原来的2倍,再向左平移 个单位得到函数 的图象,则函数 ( )A、 B、 C、 D、9. 设 的内角 所对的边分别为 ,且 已知 的面积 ,则 的值为( )A、 B、 C、 D、10. 关于数列 ,给出下列命题:①数列 满足 ,则数列 为公比为2的等比数列;②“ , 的等比中项为 ”是“ ”的充分不必要条件:③数列 是公比为 的等比数列,则其前 项和 ;④等比数列 的前 项和为 ,则 , , 成等比数列,其中假命题的序号是( )A、② B、②④ C、①②④ D、①③④11. 已知函数 ,若函数 ( 为常数)有三个零点,则实数 的取值范围为( )A、 B、 C、 D、12. 定义域为 的函数 图像的两个端点为 、 ,向量 , 是 图像上任意一点,其中 ,若不等式 恒成立,则称函数 在 上满足“ 范围线性近似”,其中最小正实数 称为该函数的线性近似阈值.若函数 定义在 上,则该函数的线性近似阈值是( )A、 B、 C、 D、二、填空题
-
13. 已知函数 ,若 ,则实数 的值是 .14. 已知 ,且 ,则当 取得最小值时相应的 .15. 已知定义在 上的可导函数 的导函数为 ,满足 且 ,则不等式 ( 为自然对数的底数)的解集是.16. 中,内角 所对的边分别为 ,若 是 与 的等比中项,且 是 与 的等差中项,则 , .
三、解答题
-
17. 已知集合 ,集合 .若命题 ,命题 ,且 是 的充分不必要条件,求实数 的取值范围.18. 在 中,角 所对的边分别为 ,满足 .(1)、求 的值;(2)、若 ,求 的取值范围19. 已知函数 .(1)、求 的最小正周期;(2)、求 在区间 上对称轴、对称中心及其最值.20. 新能源汽车是我国汽车工业由大变强的一条必经之路!国家对其给予政策上的扶持,己成为我国的战略方针.近年来,我国新能源汽车制造蓬勃发展,某著名车企自主创新,研发了一款新能源汽车,经过大数据分析获得:在某种路面上,该品牌汽车的刹车距离 (米)与其车速 (千米/小时)满足下列关系: ( , 是常数).(行驶中的新能源汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离).如图是根据多次对该新能源汽车的实验数据绘制的刹车距离 (米)与该车的车速 (千米/小时)的关系图.该新能源汽车销售公司为满足市场需求,国庆期间在甲、乙两地同时展销该品牌的新能源汽车,在甲地的销售利润(单位:万元)为 ,在乙地的销售利润(单位:万元)为 ,其中 为销售量(单位:辆).
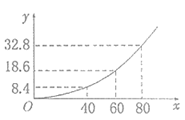 (1)、若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润 是多少?(2)、如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.
(1)、若该公司在两地共销售20辆该品牌的新能源汽车,则能获得的最大利润 是多少?(2)、如果要求刹车距离不超过25.2米,求该品牌新能源汽车行驶的最大速度.