河北省石家庄市栾城区2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
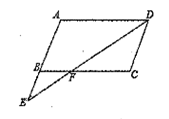
1. 点 的反比例函数 的图象上,则 的值是( )A、-6 B、-5 C、-1 D、62. 在 中, ,则 的值是( )A、 B、 C、 D、3. 如图,△ ∽△ ,若 , , ,则 的长是( )
 A、2 B、3 C、4 D、54. 甲、乙、丙、丁四人进行射击测试,经过测试,平均成绩均为 环,方差如下表所示:
A、2 B、3 C、4 D、54. 甲、乙、丙、丁四人进行射击测试,经过测试,平均成绩均为 环,方差如下表所示:选手
甲
乙
丙
丁
方差
则在这四个选手中,成绩最稳定的是( )
A、甲 B、乙 C、丙 D、丁5. 下表为某校八年级72位女生在规定时间内的立定投篮数统计,投进的个数
5
6
7
8
9
10
11
12
13
14
15
人数
3
7
6
10
11
8
13
7
1
4
2
若投篮投进个数的中位数为 ,众数为 ,则a+b的值为( )
A、20 B、21 C、22 D、236. 关于 的方程 是一元二次方程,则( )A、 B、 C、 D、7. 如果关于x的一元二次方程(m﹣3)x2+3x+m2﹣9=0有一个解是0,那么m的值是( )A、﹣3 B、3 C、±3 D、0或﹣38. 若 , 是关于 的一元二次方程 的两实根,且 ,则 等于( )A、 B、 C、2 D、39. 若 是方程 的两个实数根,则 ( )A、2018 B、2017 C、2016 D、201510. 某学校要种植一块面积为100m2的长方形草坪,要求两边长均不小于5m,则草坪的一边长为y(单位:m)随另一边长x(单位:m)的变化而变化的图象可能是( )A、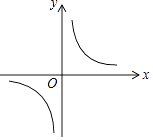 B、
B、 C、
C、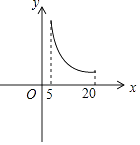 D、
D、 11. 如图,有一块三角形土地,它的底边 米,高 米,某单位要沿着底边 修一座底面是矩形 的大楼,矩形的长宽比为5:4,则这座大楼的地基面积是( )
11. 如图,有一块三角形土地,它的底边 米,高 米,某单位要沿着底边 修一座底面是矩形 的大楼,矩形的长宽比为5:4,则这座大楼的地基面积是( )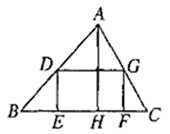 A、 B、 C、 D、12. 爱美之心人皆有之,特别是很多女士,穿上高跟鞋后往往会有很好的效果,事实上,当人体的下半身长度与身高的比值接近0.618时,会给人以美感,某女士身高165cm,下半身长与身高的比值是0.60,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A、4cm B、6cm C、8cm D、10cm
A、 B、 C、 D、12. 爱美之心人皆有之,特别是很多女士,穿上高跟鞋后往往会有很好的效果,事实上,当人体的下半身长度与身高的比值接近0.618时,会给人以美感,某女士身高165cm,下半身长与身高的比值是0.60,为了尽可能达到好的效果,她应穿的高跟鞋的高度大约为( )A、4cm B、6cm C、8cm D、10cm二、填空题
-
13. 某校开展了主题为“青春˙梦想”的艺术作品征集活动,从九年级五个班收集到的作品数量(单位:件)分别为:42,50,45,46,50,则这组数据的中位数是。14. 如果反比例函数y= (k是常数,k≠0)的图象经过点(2,3),那么在这个函数图象所在的每个象限内,y的值随x值的增大而 . (填“增大”或“减小”)15. 某校征集校运会会徽,遴选出甲、乙、丙三种图案.为了解何种图案更受欢迎,随机调查了该校100名学生,其中60名同学喜欢甲图案,若该校共有2000人,根据所学的统计知识可以估计该校喜欢甲图案的学生有人.16. 在△ABC中∠C=90°,tanA= ,则cosB=.17. 。18. 如图,已知△ABC中D为AC中点,AB=5,AC=7,∠AED=∠C,则BE=.
 19. 已知方程x2﹣10x+24=0的两个根是一个等腰三角形的两边长,则这个等腰三角形的周长为 .
19. 已知方程x2﹣10x+24=0的两个根是一个等腰三角形的两边长,则这个等腰三角形的周长为 .
20. 若代数式 可化为 ,则 = , =.三、解答题
-
21. 在一次聚会上,规定每两个人见面必须握手,且握手1次.(1)、若参加聚会的人数为3,则共握手次;若参加聚会的人数为5,则共握手次;(2)、若参加聚会的人数为n(n为正整数),则共握手次;(3)、若参加聚会的人共握手28次,请求出参加聚会的人数.(4)、嘉嘉由握手问题想到了一个数学问题:若线段AB上共有m个点(不含端点A , B),线段总数为多少呢?请直接写出结论.22. 在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
 (1)、这次调查获取的样本容量是 . (直接写出结果)(2)、这次调查获取的样本数据的众数是 , 中位数是 . (直接写出结果)(3)、若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.23. 如图,一次函数 与反比例函数 的图象交于 两点,交 轴于点 。
(1)、这次调查获取的样本容量是 . (直接写出结果)(2)、这次调查获取的样本数据的众数是 , 中位数是 . (直接写出结果)(3)、若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.23. 如图,一次函数 与反比例函数 的图象交于 两点,交 轴于点 。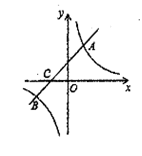 (1)、求 的值;(2)、请直接写出不等式 的解集;
(1)、求 的值;(2)、请直接写出不等式 的解集;