河北省保定市定州市2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
1. 抛物线y=x2+1的对称轴是( )A、直线x=﹣1 B、直线x=1 C、直线x=0 D、直线y=12. 点P(2,﹣1)关于原点对称的点P′的坐标是( )A、(﹣2,1) B、(﹣2,﹣1) C、(﹣1,2) D、(1,﹣2)3. 下列App图标中,既不是中心对称图形也不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、5. 如图,BC是⊙O的弦,OA⊥BC,∠AOB=70°,则∠ADC的度数是( )
4. 用配方法解方程 ,配方正确的是( )A、 B、 C、 D、5. 如图,BC是⊙O的弦,OA⊥BC,∠AOB=70°,则∠ADC的度数是( )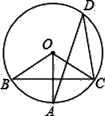 A、70° B、35° C、45° D、60°6. 下图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是( )A、
A、70° B、35° C、45° D、60°6. 下图是几种汽车轮毂的图案,图案绕中心旋转90°后能与原来的图案重合的是( )A、 B、
B、 C、
C、 D、
D、 7. 若x=﹣1是关于x的一元二次方程ax2﹣bx﹣2019=0的一个解,则1+a+b的值是( )A、2017 B、2018 C、2019 D、20208. 关于x的一元二次方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且9. 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是( )
7. 若x=﹣1是关于x的一元二次方程ax2﹣bx﹣2019=0的一个解,则1+a+b的值是( )A、2017 B、2018 C、2019 D、20208. 关于x的一元二次方程 有实数根,则k的取值范围是( )A、 B、 且 C、 D、 且9. 如图,AB是⊙O的弦,AB=5,点C是⊙O上的一个动点,且∠ACB=45°,若点M、N分别是AB、AC的中点,则MN长的最大值是( )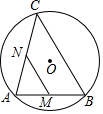 A、 B、5 C、 D、310. 如图,⊙O的半径为1,动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒B点P位于点C的位置,……,则第2017秒点P所在位置的坐标为( )
A、 B、5 C、 D、310. 如图,⊙O的半径为1,动点P从点A处沿圆周以每秒45°圆心角的速度逆时针匀速运动,即第1秒点P位于如图所示位置,第2秒B点P位于点C的位置,……,则第2017秒点P所在位置的坐标为( )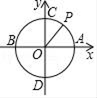 A、( , ) B、(- , ) C、(0,﹣1) D、( ,- )11. 某公司一月份获利400万元,计划第一季度的利润达到1324万元.若该公司每月的增长率相同,则该增长率是( )A、 B、 C、 D、
A、( , ) B、(- , ) C、(0,﹣1) D、( ,- )11. 某公司一月份获利400万元,计划第一季度的利润达到1324万元.若该公司每月的增长率相同,则该增长率是( )A、 B、 C、 D、二、填空题
-
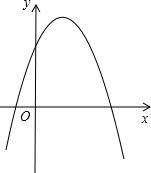
12. 已知关于x的方程x2+mx-6=0的一个根为2,则m= .13. 已知x1、x2是一元二次方程x2+x+m=0的两个根,且x1+x2=2+x1x2 , 则m= .14. 若二次函数y=ax2+bx+c的图象如图所示,则ac0(填“>”或“=”或“<”).
 15. 如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .
15. 如图,在半径为10cm的圆形铁片上切下一块高为4cm的弓形铁片,则弓形弦AB的长为 .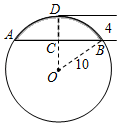 16. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD , 则∠BDC的度数为度.
16. 如图,把一个直角三角尺ACB绕着30°角的顶点B顺时针旋转,使得点A与CB的延长线上的点E重合连接CD , 则∠BDC的度数为度.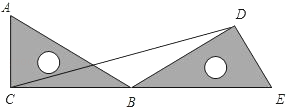 17. 元旦到了,九(2)班每个同学都与全班同学交换一件自制的小礼物,结果全班交换小礼物共1560件,该班有个同学.
17. 元旦到了,九(2)班每个同学都与全班同学交换一件自制的小礼物,结果全班交换小礼物共1560件,该班有个同学.三、解答题
-
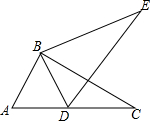
18. 解下列一元二次方程.(1)、x2-8x+1=0;(2)、2x2+1=3x.19. 已知关于x的一元二次方程 .(1)、求证:此方程总有两个实数根;(2)、若此方程有两个不相等的整数根,请选择一个合适的n值,写出这个方程并求出此时方程的根.20. 如图,将△ABC绕点B旋转得到△DBE,且A,D,C三点在同一条直线上.求证:DB平分∠ADE.
 21. 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.
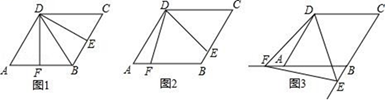
21. 如图,半径为5的⊙A中,弦BC、ED所对的圆心角分别是∠BAC,∠EAD,已知DE=6,∠BAC+∠EAD=180°.求点A到弦BC的距离.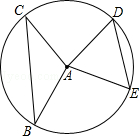 22. 在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A , B(点A在点B的左侧)(1)、当a=﹣1时,求A , B两点的坐标;(2)、过点P(3,0)作垂直于x轴的直线l , 交抛物线于点C . 当a=2时,求PB+PC的值.23. 如图,四边形 ABCD 是边长为 2,一个锐角等于 60°的菱形纸片,将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点 D 重合,按顺时针方向旋转这个三角形纸片,使它的两边分别交 CB,BA(或它们的延长线)于点 E, F;
22. 在平面直角坐标系xOy中,抛物线y=ax2﹣2x(a≠0)与x轴交于点A , B(点A在点B的左侧)(1)、当a=﹣1时,求A , B两点的坐标;(2)、过点P(3,0)作垂直于x轴的直线l , 交抛物线于点C . 当a=2时,求PB+PC的值.23. 如图,四边形 ABCD 是边长为 2,一个锐角等于 60°的菱形纸片,将一个∠EDF=60°的三角形纸片的一个顶点与该菱形顶点 D 重合,按顺时针方向旋转这个三角形纸片,使它的两边分别交 CB,BA(或它们的延长线)于点 E, F;①当 CE=AF 时,如图①,写出DE与DF的数量关系
②继续旋转三角形纸片,当 CE≠AF 时,如图②,①的结论是否成立?若成立,加以证明;若不成立,请说明理由;
③再次旋转三角形纸片,当点 E,F 分别在 CB,BA 的延长线上时,如图③, 请直接写出 DE 与 DF 的数量关系.
 24. 某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.
24. 某农场要建一个饲养场(长方形ABCD),饲养场的一面靠墙(墙最大可用长度为27米),另三边用木栏围成,中间也用木栏隔开,分成两个场地,并在如图所示的三处各留1米宽的门(不用木栏),建成后木栏总长57米,设饲养场(长方形ABCD)的宽为a米.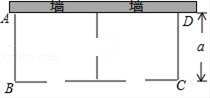 (1)、饲养场的长为多少米(用含a的代数式表示).(2)、若饲养场的面积为288m2 , 求a的值.(3)、当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?25. 如图,抛物线y=
(1)、饲养场的长为多少米(用含a的代数式表示).(2)、若饲养场的面积为288m2 , 求a的值.(3)、当a为何值时,饲养场的面积最大,此时饲养场达到的最大面积为多少平方米?25. 如图,抛物线y=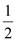 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0). 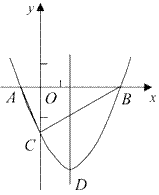 (1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m , 0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.
(1)、求抛物线的解析式及顶点D的坐标;(2)、判断△ABC的形状,证明你的结论;(3)、点M(m , 0)是x轴上的一个动点,当CM+DM的值最小时,求m的值.