北京市房山区2019-2020学年九年级上学期数学期中考试试卷
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
1. 下列各组中的四条线段成比例的是( ).A、1cm,2cm,20cm,40cm B、1cm,2cm,3cm,4cm C、4cm,2cm,1cm,3cm D、5cm,10cm,15cm,20cm2. 下列各组图形一定相似的是( )。A、任意两个平行四边形 B、任意两个矩形 C、任意两个菱形 D、任意两个正方形3. 如图,△ABC∽△AED,∠ADE=80°,∠A=60°,则∠C等于( )
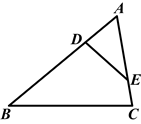 A、40° B、60° C、80° D、100°4. 对于二次函数y=﹣2x2 , 下列结论正确的是( )A、y随x的增大而增大 B、图象关于直线x=0对称 C、图象开口向上 D、无论x取何值,y的值总是负数5. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )
A、40° B、60° C、80° D、100°4. 对于二次函数y=﹣2x2 , 下列结论正确的是( )A、y随x的增大而增大 B、图象关于直线x=0对称 C、图象开口向上 D、无论x取何值,y的值总是负数5. 已知二次函数y=ax2+bx+c的图象如图所示,则下列结论正确的是( )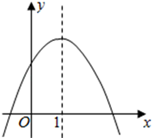 A、a+b+c>0 B、a>0 C、b2﹣4ac<0 D、c<06. 如图,小正方形的边长为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( )
A、a+b+c>0 B、a>0 C、b2﹣4ac<0 D、c<06. 如图,小正方形的边长为1,则下列图形中的三角形(阴影部分)与△ABC相似的是( ) A、
A、 B、
B、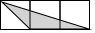 C、
C、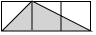 D、
D、 7. 如图,在△ABC中,D、E分别是BC、AC上的点,且DE∥AB,若S△CDE :S△BDE=1:3,则S△CDE:S△ABE =( )
7. 如图,在△ABC中,D、E分别是BC、AC上的点,且DE∥AB,若S△CDE :S△BDE=1:3,则S△CDE:S△ABE =( ) A、1:9 B、1:12 C、1:16 D、1:208.
A、1:9 B、1:12 C、1:16 D、1:208.如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴只有一个交点M,与平行于x轴的直线l交于A、B两点,若AB=3,则点M到直线l的距离为( )
 A、 B、 C、2 D、
A、 B、 C、2 D、二、填空题
-
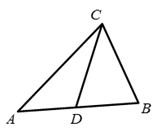
9. 如图,D是△ABC的边AB上的点,请你添加一个条件,使△CBD与△ABC相似,你添加的条件是 .
 10. 如图所示为农村一古老的捣碎器,已知支撑柱 的高为 米,踏板 长为 米,支撑点 到踏脚 的距离为 米,现在踏脚着地,则捣头点 上升了米.
10. 如图所示为农村一古老的捣碎器,已知支撑柱 的高为 米,踏板 长为 米,支撑点 到踏脚 的距离为 米,现在踏脚着地,则捣头点 上升了米.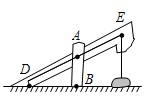 11.
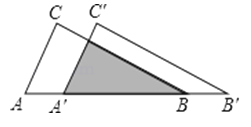
11.如图,把△ABC沿AB边平移到△A′B′C′的位置,它们的重叠部分(即图中的阴影部分)的面积是△ABC的面积的一半,若AB= , 则此三角形移动的距离AA′= .
 12. 请写出一个对称轴为x=3的抛物线的解析式 .13. 已知点A(4, ),B(1, ),C(﹣3, )在函数 (m为常数)的图象上,则 , , 的大小关系是(由小到大排列)14. 抛物线y=(x﹣1)2 + t 与x轴的两个交点之间的距离为4,则y的最小值是 .15. 在平面直角坐标系xOy中,点A(m,n)在抛物线y=ax2 +2ax-3a上,点A关于此抛物线对称轴的对称点为B(p,q),则m+p的值是 .16. 二次函数y=2x2 - 4x+m满足以下条件: 当-2<x<-1时,它的图象位于x轴的上方,当2<x<3时,它的图象位于x轴的下方,则m的值为.17. 如图,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1 , B1 , C1 , 三点都在格点上).则这个三角形的面积是
12. 请写出一个对称轴为x=3的抛物线的解析式 .13. 已知点A(4, ),B(1, ),C(﹣3, )在函数 (m为常数)的图象上,则 , , 的大小关系是(由小到大排列)14. 抛物线y=(x﹣1)2 + t 与x轴的两个交点之间的距离为4,则y的最小值是 .15. 在平面直角坐标系xOy中,点A(m,n)在抛物线y=ax2 +2ax-3a上,点A关于此抛物线对称轴的对称点为B(p,q),则m+p的值是 .16. 二次函数y=2x2 - 4x+m满足以下条件: 当-2<x<-1时,它的图象位于x轴的上方,当2<x<3时,它的图象位于x轴的下方,则m的值为.17. 如图,在由边长为1的25个小正方形组成的正方形网格上有一个△ABC,在这个网格上画一个与△ABC相似,且面积最大的△A1B1C1(A1 , B1 , C1 , 三点都在格点上).则这个三角形的面积是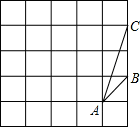
三、解答题
-
18. 若二次函数y= x2 +bx+c的图象经过点 (0,1)和 (1,2)两点,(1)、求此二次函数的表达式.(2)、当x取何值时,y随x的增大而减小.19. 已知二次函数y= x2 - 6x+10
 (1)、将其化为y=a(x-h)2+k的形式;(2)、画出其函数图象;(3)、根据图象直接写出当y>2时x的取值范围.20. 下表是二次函数y=ax2+bx+c的部分x,y的对应值:
(1)、将其化为y=a(x-h)2+k的形式;(2)、画出其函数图象;(3)、根据图象直接写出当y>2时x的取值范围.20. 下表是二次函数y=ax2+bx+c的部分x,y的对应值:x
…
﹣1
﹣
0
1
2
3
…
y
…
m
﹣1
﹣2
﹣1
2
…
(1)、二次函数图象的开口向 , 顶点坐标是 , m的值为;(2)、当x>0时,y的取值范围是;(3)、当抛物线y=ax2+bx+c的顶点在直线y=x+n的下方时,n的取值范围是 .21. 如图,△ABC中,∠ACB=90°,CD⊥AB于点D. 求证:DC 2 = DA·DB 22. 如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD、BE交于点O,连接D、E.
22. 如图,△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD、BE交于点O,连接D、E. (1)、依题意补全图形;(2)、△OAB与△OED相似吗?说明理由.23. 如图,平行四边形ABCD中,过点C作CE交BD于点M,交AD于点F,交BA的延长线于点E,若FM =2,EF =6,求CM的长.
(1)、依题意补全图形;(2)、△OAB与△OED相似吗?说明理由.23. 如图,平行四边形ABCD中,过点C作CE交BD于点M,交AD于点F,交BA的延长线于点E,若FM =2,EF =6,求CM的长.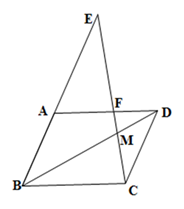 24. 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米.
24. 如图,一位运动员在距篮下4米处跳起投篮,球运行的路线是抛物线,当球运行的水平距离为2.5米时,达到最大高度3.5米,然后准确落入篮圈.已知篮圈中心到地面的距离为3.05米. (1)、建立如图所示的直角坐标系,求抛物线的表达式;(2)、该运动员身高1.7米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?.25. 有这样一个问题:探究函数y= 的图象与性质.小美根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小美的探究过程,请补充完整:
(1)、建立如图所示的直角坐标系,求抛物线的表达式;(2)、该运动员身高1.7米,在这次跳投中,球在头顶上方0.25米处出手,问:球出手时,他跳离地面的高度是多少?.25. 有这样一个问题:探究函数y= 的图象与性质.小美根据学习函数的经验,对函数y= 的图象与性质进行了探究.下面是小美的探究过程,请补充完整: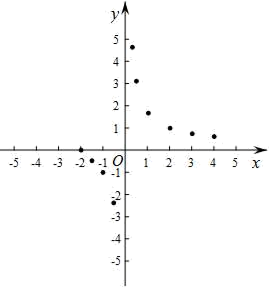 (1)、函数y= 的自变量x的取值范围是;(2)、下表是y与x的几组对应值.
(1)、函数y= 的自变量x的取值范围是;(2)、下表是y与x的几组对应值.x
﹣2
﹣
﹣1
﹣
1
2
3
4
…
y
0
﹣
﹣1
﹣
m
…
求m的值;
(3)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(4)、结合函数的图象,写出该函数的一条性质: .26. 已知抛物线C1:y1=2x2﹣4x+k与x轴只有一个公共点.(1)、求k的值;(2)、怎样平移抛物线C1就可以得到抛物线C2:y2=2(x+1)2﹣4k?请写出具体的平移方法;(3)、若点A(1,t)和点B(m,n)都在抛物线C2:y2=2(x+1)2﹣4k上,且n<t,直接写出m的取值范围.27. 如图,小芳家的落地窗(线段DE)与公路(直线PQ)互相平行,她每天做完作业后都会在点A处向窗外的公路望去.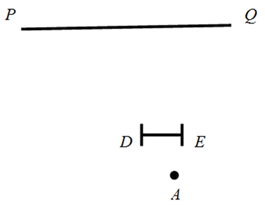 (1)、请在图中画出小芳能看到的那段公路并记为BC.(2)、小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.28. 在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.(1)、求抛物线的表达式;(2)、点D(n,y1),E(3,y2)在抛物线上,若y1<y2 , 请直接写出n的取值范围;(3)、设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.
(1)、请在图中画出小芳能看到的那段公路并记为BC.(2)、小芳很想知道点A与公路之间的距离,于是她想到了一个办法.她测出了邻家小彬在公路BC段上走过的时间为10秒,又测量了点A到窗的距离是4米,且窗DE的长为3米,若小彬步行的平均速度为1.2米/秒,请你帮助小芳计算出点A到公路的距离.28. 在平面直角坐标系xOy中,抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1.(1)、求抛物线的表达式;(2)、点D(n,y1),E(3,y2)在抛物线上,若y1<y2 , 请直接写出n的取值范围;(3)、设点M(p,q)为抛物线上的一个动点,当﹣1<p<2时,点M关于y轴的对称点都在直线y=kx﹣4的上方,求k的取值范围.