江苏省盐城市东台市第四联盟2020届九年级上学期数学期中考试试卷
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、 B、x2=0 C、x2-2y=1 D、2. 我市气象部门测得某周内六天的日温差数据如下:4,6,5,7,6,8(单位:℃).这组数据的平均数和众数分别是( )A、7,6 B、6,6 C、5,6 D、6,53.
如图,⊙O是△ABC的外接圆,若∠ABC=40°,则∠AOC的度数为( )
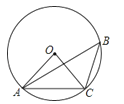 A、20° B、40° C、60° D、80°4. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)5. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=1006. 已知⊙O的直径为4,圆心O到直线l的距离是4,则⊙O与直线l的关系是( )A、相交 B、相切 C、相离 D、相交或相切7. 抛物线y=-x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )
A、20° B、40° C、60° D、80°4. 抛物线 的顶点坐标是( )A、(﹣1,2) B、(﹣1,﹣2) C、(1,﹣2) D、(1,2)5. 某种植基地2016年蔬菜产量为80吨,预计2018年蔬菜产量达到100吨,求蔬菜产量的年平均增长率,设蔬菜产量的年平均增长率为x,则可列方程为( )A、80(1+x)2=100 B、100(1﹣x)2=80 C、80(1+2x)=100 D、80(1+x2)=1006. 已知⊙O的直径为4,圆心O到直线l的距离是4,则⊙O与直线l的关系是( )A、相交 B、相切 C、相离 D、相交或相切7. 抛物线y=-x2+bx+c的部分图象如图所示,若y<0,则x的取值范围是( )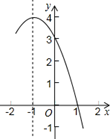 A、x<−4或x>1 B、x<−3或x>1 C、−4<x<1 D、−3<x<18. 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是( )
A、x<−4或x>1 B、x<−3或x>1 C、−4<x<1 D、−3<x<18. 如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(s).∠APB=y(°),则下列图象中表示y与t之间函数关系最恰当的是( )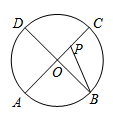 A、
A、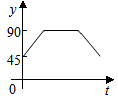 B、
B、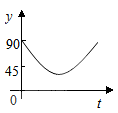 C、
C、 D、
D、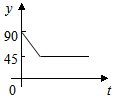
二、填空题
-
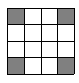
9. 方程x2=2x的解是.10. 一只自由飞行的小鸟,如果随意落在如图所示的方格地面上(每个小方格形状完全相同),那么小鸟落在阴影方格地面上的概率是 .
 11. 设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=(x+1)2+2上的三点,则y1 , y2 , y3的大小关系为.(用>号连接).12.
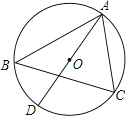
11. 设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=(x+1)2+2上的三点,则y1 , y2 , y3的大小关系为.(用>号连接).12.如图,△ABC是⊙O的内接三角形,AD是⊙O的直径,∠ABC=50°,则∠CAD= .
 13. 圆锥的底面半径是8cm,母线是6cm,则圆锥的侧面积是cm2.(结果保留π).14. 若二次函数 的图象与x轴只有一个公共点,则实数n=.15. 下列四个函数:① ② ③ ④ 中,当x<0时,y随x的增大而增大的函数是(选填序号).16. 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.点M为直线AB上一动点,点N为抛物线上一动点,当以点M,N,D,E为顶点的四边形是平行四边形时点N的坐标为.
13. 圆锥的底面半径是8cm,母线是6cm,则圆锥的侧面积是cm2.(结果保留π).14. 若二次函数 的图象与x轴只有一个公共点,则实数n=.15. 下列四个函数:① ② ③ ④ 中,当x<0时,y随x的增大而增大的函数是(选填序号).16. 边长为2的正方形OABC在平面直角坐标系中的位置如图所示,点D是边OA的中点,连接CD,点E在第一象限,且DE⊥DC,DE=DC.以直线AB为对称轴的抛物线过C,E两点.点M为直线AB上一动点,点N为抛物线上一动点,当以点M,N,D,E为顶点的四边形是平行四边形时点N的坐标为.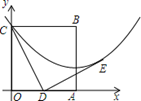
三、解答题
-
17. 解方程(1)、(2)、18. 教室讲台上粉笔盒中有红粉笔1支,黄粉笔1支,白粉笔2支,这些粉笔除颜色外其余都相同.(1)、小亮认为从粉笔盒中随机拿一支,只有红、黄、白三种可能,所以拿到红粉笔的概率是 ,你同意小亮的看法吗?(填“同意”或“不同意”);(2)、李老师在上课前,随机中粉笔盒中拿出两支粉笔,求他拿到都是白粉笔的概率,请用树状图或列表法说明.19. 希望中学八年级学生开展踢毽子活动,每班派5名学生参加,按团体总分排列名次,在规定时间内每人踢100个以上(含100)为优秀.下表是成绩较好的甲班和乙班5名学生的比赛成绩(单位:个)
1号
2号
3号
4号
5号
总数
甲班
100
98
110
89
103
500
乙班
89
100
95
119
97
500
经统计发现两班5名学生踢毽子的总个数相等.此时有学生建议,可以通过考查数据中的其它信息作为参考.请你回答下列问题:
(1)、求两班比赛数据的中位数;(2)、计算两班比赛数据的方差,并比较哪一个小;(3)、根据以上信息,你认为应该把冠军奖状发给哪一个班?简述理由.20. 已知关于x的一元二次方程(a+c)x2+2bx+(a-c)=0,其中a , b , c分别为△ABC三边的长.(1)、如果x=-1是方程的根,试判断△ABC的形状,并说明理由;(2)、如果方程有两个相等的实数根,试判断△ABC的形状,并说明理由.21. 如图,AB是⊙O的弦,AB=4,点P在 上运动,且∠APB=30°. (1)、求⊙O的半径;(2)、求图中阴影部分的面积.22. 如图,直线 和抛物线 都经过点A(2,0)和点B(k, ).
(1)、求⊙O的半径;(2)、求图中阴影部分的面积.22. 如图,直线 和抛物线 都经过点A(2,0)和点B(k, ).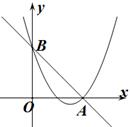 (1)、求抛物线的解析式;(2)、利用图像回答:当y1<y2时,x的取值范围是.23. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价x元,则平均每天销售数量为件(用含x的代数式表示):(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?24. 如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.
(1)、求抛物线的解析式;(2)、利用图像回答:当y1<y2时,x的取值范围是.23. 一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售、增加盈利,该店采取了降价措施,在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.(1)、若降价x元,则平均每天销售数量为件(用含x的代数式表示):(2)、当每件商品降价多少元时,该商店每天销售利润为1200元?24. 如图,AB为⊙O的直径,点D在⊙O外,∠BAD的平分线与⊙O交于点C,连接BC、CD,且∠D=90°.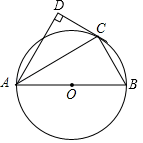 (1)、求证:CD是⊙O的切线;(2)、若∠DCA=60°,BC=3,求 的长.25. 已知关于 的一元二次方程 有实数根, 为正整数.
(1)、求证:CD是⊙O的切线;(2)、若∠DCA=60°,BC=3,求 的长.25. 已知关于 的一元二次方程 有实数根, 为正整数. (1)、求 的值;(2)、当此方程有两个不为0的整数根时,将关于 的二次函数 的图象向下平移2个单位,求平移后的函数图象的解析式;(3)、在(2)的条件下,将平移后的二次函数图象位于 轴左侧的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出 的取值范围.26. 张老师给爱好学习的的小军和小俊提出这样一个问题:如图(1),在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.
(1)、求 的值;(2)、当此方程有两个不为0的整数根时,将关于 的二次函数 的图象向下平移2个单位,求平移后的函数图象的解析式;(3)、在(2)的条件下,将平移后的二次函数图象位于 轴左侧的部分沿 轴翻折,图象的其余部分保持不变,得到一个新的图象G.当直线 与图象G有3个公共点时,请你直接写出 的取值范围.26. 张老师给爱好学习的的小军和小俊提出这样一个问题:如图(1),在△ABC中,AB=AC,点P为边BC上的任一点,过点P作PD⊥AB,PE⊥AC,垂足分别为D,E,过点C作CF⊥AB,垂足为F.求证:PD+PE=CF.小军的证明思路是:如图(2),连接AP,由△ABP与△ACP面积之和等于△ABC的面积可以证得:PD+PE=CF.
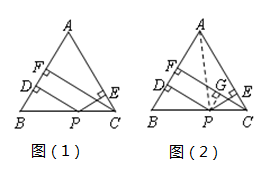
老师表扬了小军,并且告诉小军和小俊:在求解平面几何问题的时候,根据有关几何量与涉及的有关图形面积之间的内在联系,用面积或面积之间的关系表示有关线段间的关系,从而把要论证的线段之间的关系转化为面积的关系,并通过图形面积的等积变换对所论问题来进行求解的方法,这种方法称为“面积法”.
请你使用“面积法”解决下列问题:
(1)、Rt△ABC两条直角边长为3和4,则它的内切圆半径为;(2)、如图(3),△ABC中AB=15,BC=14,AC=13,AD是BC边上的高.求AD长及△ABC的内切圆的半径;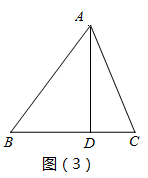 (3)、如图(4),在四边形ABCD中,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,⊙O1与△ABD切点分别为E、F、G,设它们的半径分别为r1和r2 , 若∠ADB=90°,AE=8,BC+CD=20,S△DBC=36,r2=2,求r1的值.
(3)、如图(4),在四边形ABCD中,⊙O1与⊙O2分别为△ABD与△BCD的内切圆,⊙O1与△ABD切点分别为E、F、G,设它们的半径分别为r1和r2 , 若∠ADB=90°,AE=8,BC+CD=20,S△DBC=36,r2=2,求r1的值.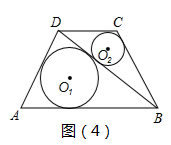 27. 如图,在平面直角坐标系中抛物线 交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
27. 如图,在平面直角坐标系中抛物线 交x轴于点A、B,交y轴于点C, A、B两点横坐标为-1和3,C点纵坐标为-4.
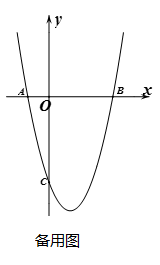 (1)、求抛物线的解析式;(2)、动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;(3)、抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.
(1)、求抛物线的解析式;(2)、动点D在第四象限且在抛物线上,当△BCD面积最大时,求D点坐标,并求△BCD面积的最大值;(3)、抛物线的对称轴上是否存在一点Q,使得∠QBC=45°,如果存在,求出点Q的坐标,不存在说明理由.