江苏省无锡市宜兴市宜城环科园联盟2020届九年级上学期数学期中考试试卷
试卷更新日期:2019-12-05 类型:期中考试
一、单选题
-
1. 下列方程是一元二次方程的是( )A、x -2x-1=0 B、 =1 C、(x-1) +y =2 D、(x-1)(x-3)=x2. 若关于x的方程x2-4x+m=0有两个相等的实数根,则m的值是( )A、1 B、2 C、4 D、±43. 某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ).A、20% B、40% C、18% D、36%4. 如图,四边形ABCD内接于⊙O,若∠A=40°,则∠C=( )
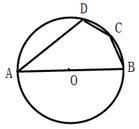 A、110° B、120° C、135° D、140°5. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( )
A、110° B、120° C、135° D、140°5. 如图,AB是⊙O的直径,CD是⊙O的弦,∠ACD=30°,则∠BAD为( ) A、30° B、50° C、60° D、70°6. 如图,在⊙ 中,半径 垂直弦 于 ,点 在⊙ 上, ,则半径 等于( )
A、30° B、50° C、60° D、70°6. 如图,在⊙ 中,半径 垂直弦 于 ,点 在⊙ 上, ,则半径 等于( )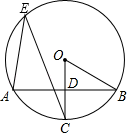 A、 B、 C、 D、7. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( )
A、 B、 C、 D、7. 如图,每个小正方形的边长均为1,则下列图形中的三角形(阴影部分)与 相似的是( ) A、
A、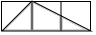 B、
B、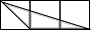 C、
C、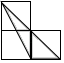 D、
D、 8. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )
8. 如图, ,直线 、 与这三条平行线分别交于点 、 、 和点 、 、 .已知 , , ,则 的长为( )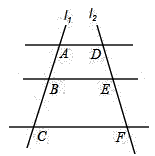 A、3.6 B、4.8 C、5 D、5,29. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )
A、3.6 B、4.8 C、5 D、5,29. 如图,在 中,点 , 分别在 , 边上, , ,若 , ,则线段 的长为( )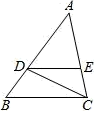 A、 B、 C、 D、510. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )
A、 B、 C、 D、510. 如图,在平面直角坐标系中,已知点A(1,0),B(1﹣a,0),C(1+a,0)(a>0),点P在以D(4,4)为圆心,1为半径的圆上运动,且始终满足∠BPC=90°,则a的最大值是( )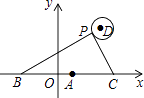 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
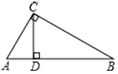
11. 在1:500000的无锡市地图上,新建的地铁线估计长5cm,那么等地铁造好后实际长约为千米.12. 若方程(m+2)x2+5x﹣7=0是关于x的一元二次方程,则m≠.13. 已知⊙O的半径为5,若圆心O到弦AB的距离为3,则AB=.14. 如图,在Rt△ABC中,∠ACB=90°,点D是边AB上的一点,CD⊥AB于D,AD=2,BD=6,则边AC的长为.
 15. 如图,AD是⊙O的直径, ,若∠AOB=40º,则圆周角∠BPC=.
15. 如图,AD是⊙O的直径, ,若∠AOB=40º,则圆周角∠BPC=. 16. 如图, 与 是以点 为位似中心的位似图形,相似比为 , , ,若点 的坐标是 ,则点 的坐标是.
16. 如图, 与 是以点 为位似中心的位似图形,相似比为 , , ,若点 的坐标是 ,则点 的坐标是.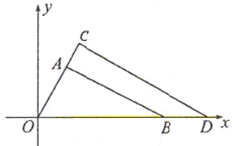 17. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .
17. 如图,在矩形 中, ,点 是 的中点,点 在 上, ,点 、 在线段 上.若 是等腰三角形且底角与 相等,则 .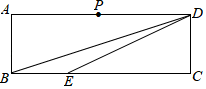 18. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为.
18. 如图,在矩形ABCD中, , ,点E在边BC上,且 .连接AE,将 沿AE折叠,若点B的对应点 落在矩形ABCD的边上,则a的值为.
三、解答题
-
19. 解方程:(1)、(x-1)2=4
(2)、x2-3x-2=0(3)、x2+6x=7(4)、2(x2-x)-(x-1)(x+3)+1=020. 已知关于x的一元二次方程(a-3)x2+x+a2―a―6=0的一个根是0,试解方程(a2-1)x2+ax―1=0.21. 为加快新旧动能转换,提高公司经济效益,某公司决定对近期研发出的一种电子产品进行降价促销,使生产的电子产品能够及时售出,根据市场调查:这种电子产品销售单价定为 元时,每天可售出 个;若销售单价每降低 元,每天可多售出 个.已知每个电子产品的固定成本为 元,问这种电子产品降价后的销售单价为多少元时,公司每天可获利 元?22. 如图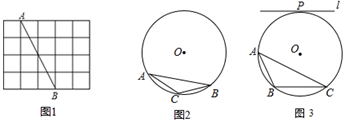 (1)、如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为.请借助网格,仅用无刻度的直尺在AB上作出点P,使AP= .(2)、⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).
(1)、如图1,网格中每个小正方形的边长为1,点A,B均在格点上.则线段AB的长为.请借助网格,仅用无刻度的直尺在AB上作出点P,使AP= .(2)、⊙O为△ABC的外接圆,请仅用无刻度的直尺,依下列条件分别在图2,图3的圆中画出一条弦,使这条弦将△ABC分成面积相等的两部分(保留作图痕迹,不写作法,请下结论注明你所画的弦).①如图2,AC=BC;
②如图3,P为圆上一点,直线l⊥OP且l∥BC.
23. 如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N. (1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长.24. 如图,在平面直角坐标系中,以点M(0, )为圆心,以 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E.
(1)、求证:△ABM∽△EFA;(2)、若AB=12,BM=5,求DE的长.24. 如图,在平面直角坐标系中,以点M(0, )为圆心,以 长为半径作⊙M交x轴于A,B两点,交y轴于C,D两点,连接AM并延长交⊙M于P点,连接PC交x轴于E. (1)、求出CP所在直线的解析式;(2)、连接AC,请求△ACP的面积.25. 在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.
(1)、求出CP所在直线的解析式;(2)、连接AC,请求△ACP的面积.25. 在解决数学问题时,我们常常从特殊入手,猜想结论,并尝试发现解决问题的策略与方法.【问题提出】
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形的对边的平方和是一个定值.
(1)、【从特殊入手】我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.
请你在图①中补全特殊殊位置时的图形,并借助于所画图形探究问题的结论.
 (2)、【问题解决】
(2)、【问题解决】已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证:
证明:
 26. 如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连结DP.
26. 如图,在矩形ABCD中,AB=4,BC=3,点P是边AB上的一动点,连结DP.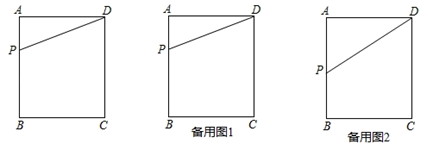 (1)、若将△DAP沿DP折叠,点A落在矩形的对角线上点A′处,试求AP的长;(2)、点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处,若P,A′,B′三点恰好在同一直线上,且A′B′=2,试求此时AP的长;(3)、当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,连结CF,请求出CF的长.
(1)、若将△DAP沿DP折叠,点A落在矩形的对角线上点A′处,试求AP的长;(2)、点P运动到某一时刻,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A′,B′处,若P,A′,B′三点恰好在同一直线上,且A′B′=2,试求此时AP的长;(3)、当点P运动到边AB的中点处时,过点P作直线PG交BC于点G,将△DAP与△PBG分别沿DP与PG折叠,点A与点B重合于点F处,连结CF,请求出CF的长.