江苏省无锡市江阴市华士片2020届九年级上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各数中，负数是（）．

A、 $- (- 2)$ B、 $- | - 2 |$ C、 ${(- 2)}^{2}$ D、 ${(- 2)}^{0}$

查看试题解析
2. 下列计算正确的是（）

A、x²+x²＝x⁵ B、x²•x³＝x⁶ C、x³÷x²＝x D、（2x²）³＝6x⁶

查看试题解析
3. 在 $△ A B C$ 中，若一个内角等于另外两个角的差，则（）

A、必有一个角等于 $30 °$ B、必有一个角等于 $45 °$ C、必有一个角等于 $60 °$ D、必有一个角等于 $90 °$

查看试题解析
4. 已知九年级某班30位同学种树72棵，男生每人种3棵，女生每人种2棵，设男生x人，则（）

A、 $2 x + 3 (72 - x) = 30$ B、 $3 x + 2 (72 - x) = 30$ C、 $2 x + 3 (30 - x) = 72$ D、 $3 x + 2 (30 - x) = 72$

查看试题解析
5. 如图，在 $△ A B C$ 中，D、E分别在AB边和AC边上， $D E / / B C$ ，M为BC边上一点（不与B，C重合），连结AM交DE于点N，则（）

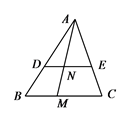A、 $\frac{A D}{A N} = \frac{A N}{A E}$ B、 $\frac{B D}{M N} = \frac{M N}{C E}$ C、 $\frac{D N}{B M} = \frac{N E}{M C}$ D、 $\frac{D N}{M C} = \frac{N E}{B M}$

查看试题解析
6. 用配方法解一元二次方程 $x^{2} - 4 x + 1 = 0$ 时，下列变形正确的是（）．

A、 ${(x - 2)}^{2} = 1$ B、 ${(x - 2)}^{2} = 5$ C、 ${(x + 2)}^{2} = 3$ D、 ${(x - 2)}^{2} = 3$

查看试题解析
7. 如图，AB是⊙O的弦，OC⊥AB，交⊙O于点C，连接OA，OB，BC，若∠ABC＝20°，则∠AOB的度数是（）

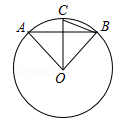A、40° B、50° C、70° D、80°

查看试题解析
8. 关于x的一元二次方程x²+kx﹣2＝0（k为实数）根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、不能确定

查看试题解析
9. 给出下列4个命题：①相似三角形的周长之比等于其相似比；②方程x²-3x+5=0的两根之积为5；③在同一个圆中，同一条弦所对的圆周角都相等；④圆的内接四边形对角互补.其中，真命题为（）

A、①②④ B、①③④ C、①④ D、①②③④

查看试题解析
10. 如图.在矩形ABCD中，AB=6，BC=8.E是边AD的一个动点，将△BAE沿BE对折至△BFE的位置，则线段DF的最小值为（）

A、2 B、4 C、6 D、8

查看试题解析

二、填空题

11. 在1：500000的无锡市地图上，新建的地铁线估计长4.5cm，那么等地铁造好后实际长约为千米。

查看试题解析
12. 如图，在△ABC中，DE∥BC，若AD=3，DB=2，则 $S_{△ A D E} ： S_{△ A B C}$ =.

查看试题解析
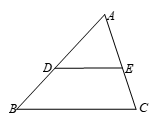13. 已知圆锥的底面半径是1cm，母线长为3cm，则该圆锥的侧面积为 cm² ．

查看试题解析
14. 一棵高 $3$ 米的小树影长为 $4$ 米，同时临近它的一座楼房的影长是 $24$ 米，这座楼房高米.

查看试题解析
15. 已知关于x的一元二次方程（a-1）x²+ 3x+a²-a=0的一个解为0，则a =.

查看试题解析
16. 如图，在⊙O中，AE是直径，半径OC垂直于弦AB于D，连接BE，若AB=2 $\sqrt{7}$ ，CD=1，则BE的长是.

查看试题解析
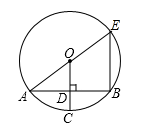17. 如图，直线y=- $\frac{3}{4}$ x-3交x轴于点A，交y轴于点B，点P是x轴上一动点，以点P为圆心，以1个单位长度为半径作⊙P，当⊙P与直线AB相切时，点P的坐标是.

查看试题解析
18. 如图，把某矩形纸片ABCD沿EF，GH折叠（点E，H在AD边上，点F，G在BC边上），使点B和点C落在AD边上同一点P处，A点的对称点为A′点，D点的对称点为D′点，若∠FPG＝90°，△A′EP的面积为5，△D′PH的面积为20，则矩形ABCD的面积等于.

查看试题解析

三、解答题

19. 计算与化简：

(1)、| $\sqrt{3}$ －2|－ $\sqrt{27}$ ＋2^-2

(2)、（x＋1）²－(x²－x)

查看试题解析
20. 解方程:

(1)、x²－2 x －5=0

(2)、4x²=（1－3x）²

查看试题解析
21. 已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是1个单位长度）.

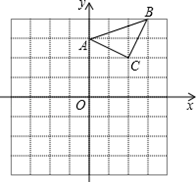(1)、①画出△ABC关于x轴的轴对称图形，得到的△A₁B₁C₁ ，点C₁的坐标是；
②以点B为位似中心，在网格内画出△A₂B₂C₂ ，使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是；

(2)、△A₂B₂C₂的面积是平方单位.

查看试题解析
22. 已知关于x的一元二次方程x²－（2m＋1）x＋m²+m＝0.

(1)、求证：该一元二次方程总有两个不相等的实数根；

(2)、若该方程的两根x₁、x₂是某个等腰三角形的两边长，且该三角形的周长为10，试求m的值.

查看试题解析
23. 如图，已知正方形ABCD的边长为1，正方形CEFG的面积为 $S_{1}$ ，点E在CD边上，点G在BC的延长线上，设以线段AD和DE为邻边的矩形的面积为 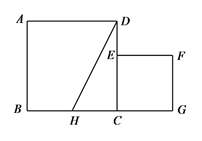$S_{2}$ ，且 $S_{1} = S_{2}$ .

(1)、求线段CE的长；

(2)、若点H为BC边的中点，连结HD，求证： $H D = H G$ .

查看试题解析
24. 如图，在 $Δ A B C$ 中， $A B = A C$ ， $A D$ 为 $B C$ 边上的中线， $D E ⊥ A B$ 于点E.

(1)、求证： $Δ B D E ∽ Δ C A D$ ；

(2)、若 $A B = 13$ ， $B C = 10$ ，求线段 $D E$ 的长.

查看试题解析
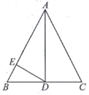25. 如图，在Rt△ACB中，∠C=90°，AC=3cm，BC=4cm，以BC为直径作⊙O交AB于点D.

(1)、求线段AD的长度；

(2)、点E是线段AC上的一点，试问：当点E在什么位置时，直线ED与⊙O相切？请说明理由.

查看试题解析
26. 某电商平台长期销售A型商品，2017年以4800元购进该型号商品并且全部售完；2019年，这种型号的商品的进价比2017年下降了9元/件，该平台用3000元购进了与2017年相同数量的该A型商品也全部售完，这两年A型商品的售价均为40元/件.

(1)、2017年A型商品的进价是多少元/件？

(2)、若该电商平台每年销售这种礼盒所获利润的年增长率相同，问年增长率是多少？

查看试题解析
27. 【定义】
数学活动课上，李老师给出如下定义：如果一个三角形有一边上的中线等于这条边的一半，那么称三角形为“智慧三角形”.

(1)、【理解】
如图，已知A，B是⊙O上两点，请在圆上找出满足条件的点C，使 $△ A B C$ 为“智慧三角形”（画出点C的位置，保留作图痕迹）；

(2)、如图2，在正方形ABCD中，E是BC的中点，F是CD上一点，且 $C F = \frac{1}{4} C D$ ，试判断 $△ A E F$ 是否为“智慧三角形”，并说明理由；
运用：

(3)、如图3，在平面直角坐标系 $x O y$ 中，⊙O的半径为，点Q是直线y=3上的一点，若在⊙O上存在一点P，使得 $△ O P Q$ 为“智慧三角形”，当其面积取得最小值时，直接写出此时点P的坐标.

查看试题解析
28. 如图，已知一次函数y=﹣ $\frac{4}{3}$ x+4的图象是直线l，设直线l分别与y轴、x轴交于点A、B.

(1)、求线段AB的长度；

(2)、设点M在射线AB上，将点M绕点A按逆时针方向旋转90°到点N，以点N为圆心，NA的长为半径作⊙N.
①当⊙N与x轴相切时，求点M的坐标；

②在①的条件下，设直线AN与x轴交于点C，与⊙N的另一个交点为D，连接MD交x轴于点E，直线m过点N分别与y轴、直线l交于点P、Q，当△APQ与△CDE相似时，求点P的坐标.

查看试题解析