浙江省衢州市六校联谊2020届九年级上学期数学期中考试试卷
试卷更新日期：2019-12-05 类型：期中考试
一、选择题（每小题3分，共30分）
-
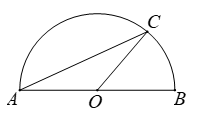
1. 下列成语所描述的事件是必然事件的是（ ）A、守株待兔 B、拔苗助长 C、瓮中捉鳖 D、水中捞月2. 抛物线y=x2－2与y轴的交点坐标是（ ）A、（0，2） B、（0，－2） C、（2，0） D、（－2，0）3. 如图，以AB为直径的半圆上有一点C，∠C=25°，则 的度数为（ ）
A、25° B、30° C、50° D、65°4. 下列二次函数的图象与x轴没有交点的是（ ）A、y=-3x2-4x B、y=x2-3x-4 C、y=x2-6x+9 D、y=2x2+4x+55. 四张质地、大小相同的卡片上，分别画上如下图所示的四种汽车标志，在看不到图形的情况下从中任意抽出一张，则抽出的卡片既是中心对称图形，又是轴对称图形的概率是（ ）
A、 B、 C、 D、16. 将抛物线y=3x2先向左平移1个单位，再向上平移1个单位，两次平移后得到的抛物线表达式为（ ）
A、y=3(x-1)2=1 B、y=3(x+1)2-1 C、 D、7. 圆内接四边形ABCD的四个内角之比可能是（ ）A、1：2：3：4 B、1：3：4：5 C、2：3：4：5 D、2：3：5：48. 点(－2， y1 )、(-3， y2 )是抛物线 上的两点，则下列正确的是（ ）
A、y1>y2 B、y2>y1 C、y1=y2 D、不确定9. 数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（ ）
A、勾股定理 B、直径所对的圆周角是直角 C、勾股定理的逆定理 D、90°的圆周角所对的弦是直径10. 在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：若y′＝ ，则称点Q为点P的“亲密点”．例如：点（1，2）的“亲密点”为点（1，3），点（﹣1，3）的“亲密点”为点（﹣1，﹣3）．若点P在函数y＝x2﹣2x﹣3的图象上，则其“亲密点”Q的纵坐标y′关于x的函数图象大致正确的是（ ）A、
B、
C、
D、
二、填空题（每小题4分，共24分）
-
11. 若抛物线y=ax2+bx+c的开口向下，则a的值可能是.（写一个即可）12. 一个正多边形的一个内角等于144°，则这个正多边形的边数为.13. 已知抛物线y=ax2+bx+c与x轴的交点是（-4,0），（2,0），则这条抛物线的对称轴是.14. 将分别标有“衢”“州” “有” “礼”汉字的四个小球装在一个不透明的口袋中，这些球除汉字外无其他差别。每次摸球前先搅拌均匀，随机摸出一球，放回；搅拌均匀，再随机摸出一球。则两次摸出的球，一个球是“衢”，一个球是“州”的概率是.15. 刻度尺与⊙O如图摆放时，有刻度的一边与⊙O的两个交点处的读数如图所示（单位：cm），圆的半径是5 cm，那么圆心到刻度尺的最近距离为
16. 如图，在平面直角坐标系xOy中，已知抛物线 y=-x(x-3)(0≤x≤3) 在x轴上方部分记作C1 ， 它与x轴交于点O，A1 ， 将C1绕点A1旋转180°得C2 ， C2与x 轴交于另一点A2 ． 继续操作并探究：将C2绕点A2旋转180°得C3 ， 与x 轴交于另一点A3；将C3绕点A 2旋转180°得C4 ， 与x 轴交于另一点A4 ， 这样依次得到x轴上的点A1 ， A2 ， A3 ， …，An ， …，及抛物线C1 ， C2 ， …，Cn ， …．则点A4的坐标为；Cn的顶点坐标为(n为正整数，用含n的代数式表示) ．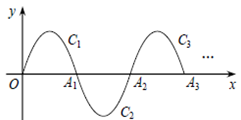
三、解答题（有8小题，共64分）
-
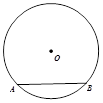
17. 已知二次函数的表达式为y=-3（x-3）2+2.(1)、写出该函数的顶点坐标；(2)、判断点（1，-12）是否在这个函数的图象上。18. 如图， 的一条弦分圆周长为1：4两部分.试求弦AB所对的圆心角和圆周角的度数（画出图形并给出解答）.
19. 如图，在单位长度为1的正方形网格中，一段圆弧经过网格的交点 A 、 、 ．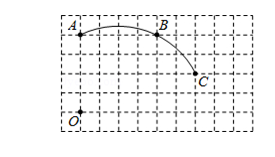
(1)、请完成如下操作：①以点 为原点、竖直和水平方向为轴、网格边长为单位长，建立平面直角坐标系；②根据图形提供的信息，标出该圆弧所在圆的圆心 ，并连结 、(2)、请在（1）的基础上，完成下列填空：①写出点的坐标： 、 ．
② 的半径 （结果保留根号）
③求出 的长．
20. “活力新衢州，美丽大花园”。衢州市某中学九年级开展了“我最喜爱的旅游景区”的抽样调查（每人只能选一项）：A﹣“世界文化新遗产”开化根博园；B﹣“首个自然遗产”江郎山；C﹣“乌溪江上的明珠”九龙湖；D﹣“世界最大的象形石动物园”三衢石林；E﹣“世界第九大奇迹”龙游石窟．根据收集的数据绘制了两幅不完整的统计图，其中B对应的圆心角为90°．请根据图中信息解答下列问题：
(1)、此次抽取的九年级学生共人，并补全条形统计图；(2)、扇形统计图中m= ， 表示E的扇形的圆心角是度；(3)、九年级准备在最喜爱A景区的4名优秀学生中任意选择两人去实地考察，这4名学生中有2名男生和2名女生，用树状图或列表法求选出的两名学生都是男生的概率．21. 某景区经营一种新上市的纪念品，进价为20元/件．试营销阶段发现：当销售单价是25元时，每天的销售量为250件；销售单价每上涨1元，每天的销售量就减少10件．设这种纪念品的销售单价为x（元）.(1)、求每天所得的销售利润y（元）与销售单价x（元）之间的函数关系式；(2)、求销售单价为多少元时，该纪念品每天的销售利润最大；(3)、若要求每天销售量不少于10件，且每件文具的利润至少为25元则该纪念品的最大利润是多少？22. 如图，AB是⊙O的直径，弦CD交AB于点E，OF⊥AC于点F，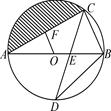
(1)、请探索OF和BC的关系，并说明理由；(2)、若∠D＝30°，BC＝1时，求圆中阴影部分的面积．(结果保留π)23. “阳光体育活动”促进了学校体育活动的开展，小杰在一次铅球比赛中，铅球出手以后的轨迹是抛物线的一部分（如图所示），已知铅球出手时离地面1.6米，铅球离投掷点3米时达到最高点，在离投掷点8米处落地，
(1)、请求出此轨迹所在抛物线的关系式.(2)、设抛物线与X轴另一个交点是E，点Q是对称轴上的一个动点，求当△EBQ的周长最短时点Q的坐标。(3)、在抛物线上是否存在点G使得S△DEG=19.5，若存在请求出点G的坐标，若不存在，请说明理由.24. 如图，四边形ABCD内接于 .
(1)、连接AC、BD，若∠BAC=∠CAD=60°，则 的形状为.(2)、在（1）的条件下，试探究线段AD，AB，AC之间的数量关系，并证明你的结论；(3)、若 = ，∠DAB=∠ABC=90°，点P为 上的一动点，连接PA，PB，PD，求证：PD=PB+ PA。