浙江省衢州市六校联谊2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-05 类型：期中考试
一、选择题（共10题，每题3分，共30分）
-
1. 下列“微信表情”中属于轴对称图形的是（ ）A、
B、 
C、
D、
2. 在下列长度的三条线段中,能组成三角形的是（ ）A、2 cm, 2cm, 4cm B、3 cm, 4cm, 6cm C、1 cm, 4cm, 6cm D、2 cm, 5cm, 7 cm3. 已知a＜b，下列不等式中正确的是（ ）A、 B、 a﹣3＜ b﹣3 C、a+3＞b+3 D、﹣3a＜﹣3b4. 已知在△ABC中，∠A=∠B —∠C，则△ABC为（ ）A、锐角三角形 B、钝角三角形 C、直角三角形 D、以上都有可能5. 下列条件不能保证两个三角形全等的是（ ）A、三边对应相等 B、两边一角对应相等 C、两角一边对应相等 D、直角边和一个锐角对应相等6. 下列命题：①同旁内角互补，两直线平行；②若|a|=|b|，则a=b；③直角都相等；④相等的角是对顶角．真命题的个数是（ ）A、4个 B、3个 C、2个 D、1个7. 同学们都玩过跷跷板的游戏，如图是一个跷跷板的示意图，立柱OC与地面垂直，OA＝OB.当跷跷板的一头A着地时，∠AOA′=50°，则当跷跷板的另一头B着地时，∠COB′等于（ ）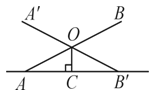
A、25° B、50° C、65° D、130°8. 如图所示，若∠A=32°，∠B=45°，∠C=38°，则∠DFE等于（ ）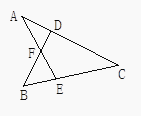
A、120° B、115° C、110° D、105°9. 如图，在△ABC中，AB＝AC＝5，BC＝6，AD是BC边上的中线，点E、F、M、N是AD上的四点，则图中阴影部分的总面积是（ ）
A、6 B、8 C、4 D、1210. 如图，∠AOB＝30º，∠AOB内有一定点P，且OP＝10．在OA上有一动点Q，OB上有一动点R．若ΔPQR周长最小，则最小周长是（ ）
A、10 B、 C、20 D、二、填空题（共6题，每小题4分，共24分）
-
11. 在Rt△ABC中, 锐角∠A＝35°，则另一个锐角∠B＝°．
12. 如图，数轴上所表示的x的取值范围为 ．
13. 已知等腰三角形的其中两边长分别为2，5，则这个等腰三角形的周长为 ．14. 如图，∠AOB=50°，CD⊥OA于D，CE⊥OB于E，且CD=CE，则∠DOC=.
15. 如图，在△ABC中，点E是BC的中点，AB=BE，BD⊥AE交AD于点D，若△ABC的面积为2，则△CDE的面积为.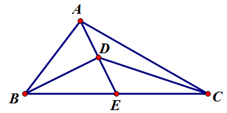
16. 如图，△ABC中，∠C＝90º，AC＝BC，AD=16cm，BE=12cm，点P是斜边AB的中点．有一把直角尺MPN，将它的顶点与点P重合，将此直角尺绕点P旋转，与两条直角边AC和CB分别交于点D和点E． 则线段PD和PE的数量关系为 ， 线段DE=cm．
三、简答题（共8题，共66分）
-
17. 解下列不等式，并把解集在数轴上表示出来(1)、2－5x≥8－2x(2)、18. 如图，在△ABC中，AB＝AC，∠ABC＝76°.
(1)、用直尺和圆规作∠ABC的平分线BD交AC于点D(保留作图痕迹，不要求写作法)；(2)、在(1)中作出∠ABC的平分线BD后，求∠BDC的度数．19. 如图，在△ABC和△DCB中，AB = DC，AC = DB，AC与DB交于点M．
(1)、求证：△ABC≌△DCB ；(2)、过点C作CN∥BD，过点B作BN∥AC，CN与BN交于点N，试判断△BNC的形状，并证明你的结论．20. 如图，花果山上有两只猴子在一棵树CD上的点B处，且BC=5m，它们都要到A处吃东西，其中一只猴子甲沿树爬下走到离树10m处的池塘A处，另一只猴子乙先爬到树顶D处后再沿缆绳DA线段滑到A处．已知两只猴子所经过的路程相等，设BD为xm．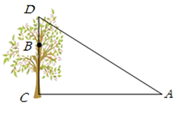
(1)、请用含有x的整式表示线段AD的长为m；(2)、求这棵树高有多少米？21. 如图 △ABC中，AB＝AC，∠A＝36º，AC的垂直平分线交AB于E，D为垂足，连结EC．
(1)、求∠ECD的度数；(2)、若CE＝5，求BC长22. 如图，已知△ABC是等边三角形，BD是AC上的高线.作AE⊥AB于点A，交BD的延长线于点E.取BE的中点M，连结AM.
(1)、求证：△AEM是等边三角形；(2)、若AE=2，求△AEM的面积.23.
(1)、【问题情境】
课外兴趣小组活动时，老师提出了如下问题：
如图①，△ABC中，若AB＝13，AC＝9，求BC边上的中线AD的取值范围．
小明在组内经过合作交流，得到了如下的解决方法：延长AD至点E，使DE＝AD，连接BE．请根据小明的方法思考：
Ⅰ.由已知和作图能得到△ADC≌△EDB，依据是 ．
A．SSS B．SAS C．AAS D．HL
Ⅱ.由“三角形的三边关系”可求得AD的取值范围是 ．
解后反思：题目中出现“中点”、“中线”等条件，可考虑延长中线构造全等三角形，把分散的已知条件和所求证的结论集中到同一个三角形之中．(2)、【初步运用】如图②，AD是△ABC的中线，BE交AC于E，交AD于F，且∠FAE＝∠AFE．若AE＝4，EC＝3，求线段BF的长．
24. 如图，△ABC中，∠ACB＝90°，AB＝5cm，BC＝4cm，若点P从点A出发，以每秒1cm的速度沿折线A﹣B﹣C﹣A运动，设运动时间为t（t＞0）秒．
(1)、AC＝cm；(2)、若点P恰好在AB的垂直平分线上，求此时t的值；(3)、在运动过程中，当t为何值时，△ACP是以AC为腰的等腰三角形（直接写出结果）？