浙江省湖州市长兴县2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-05 类型：期中考试
一、选择题(每小题3分，共30分)
-
1. 在△ABC中，∠A=35°，∠B=80°，则∠C=（ ）A、85° B、75° C、65° D、55°2. 在Rt△ABC中，两直角边长分别为3和4，则斜边的长度是（ ）A、2 B、 C、5 D、 或53. 在美术字“中华人民共和国成立七十周年”中，可以看作是轴对称图形的有（ ）A、3个 B、4个 C、5个 D、6个4. 尺规作图作∠AOB的平分线方法如下：如图，以点O为圆心，任意长为半径画弧分别交OA，OB于点C，D，再分别以点C，D为圆心，以大于 CD长为半径画弧，两弧交于点P，作射线OP，由作法得△OCP≌△ODP的根据是（ ）
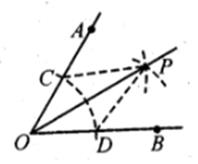A、SSS B、ASA C、AAS D、SAS5. 如图，D在AB上，E在AC上，且∠B=∠C，则再添加下列条件，仍无法判定△ABE≌△ACD的是（ ）
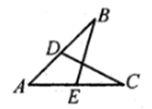A、AD=AE B、AB=AC C、BE=CD D、∠AEB=∠ADC6. 已知a>b，则下列不等式不成立的是（ ）A、3a>3b B、b+3<a+3 C、-a>-b D、3-2a<3-2b7. 如图，在Rt△ABC中，∠ACB=90°，分别以点B和点C为圆心，大于 BC的长为半径作弧，两弧相交于D、E两点，作直线DE交AB于点F，交BC于点G，连结CF．若AC =3，CG=2，则CF的长为（ ）
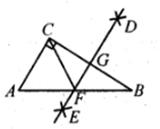A、2.5 B、3 C、2 D、3.58. 将一副三角板(∠A=30°，∠E=45°)按如图所示方式摆放，使得BA∥EF，则∠AOF等于（ ）
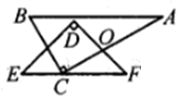A、60° B、75° C、105° D、115°9. 如图，在△ABC中，AC=BC，点D和E分别在AB和AC上，且AD=AE．连结DE，过点A的直线GH与DE平行，若∠C=40°，则∠GAD的度数为 （ ）
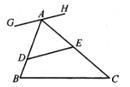A、40° B、45° C、55° D、70°10. 如图，对角线AC将正方形ABCD分成两个等腰三角形，点E，F将对角线AC三等分，且AC=15，点P在正方形的边上，则满足PE+PF=5 的点P的个数是（ ）
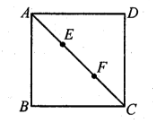A、0 B、4 C、8 D、16二、填空题(每小题4分，共24分)
-
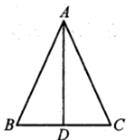
11. “y减去1不大于2”用不等式表示为： ．12. 等腰三角形的两边长为3和6，则这个等腰三角形的周长是 ．13. ”两个全等的三角形的周长相等“的逆命题是命题。（填”真“或”假“）。14. 如图，在△ABC中，AB=AC，BD=CD，∠B=70°，则∠BAD=。
15. 如图，已知OP平分∠AOB，CP∥OA，PD⊥OA于点D，PE⊥OB于点E．CP= ，PD=6。如果点M是OP的中点，则DM的长是。
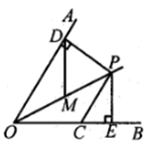16. 如图是“赵爽弦图”，△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形．如果AB=13，EF=7，那么AH等于。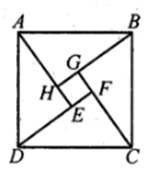
三、解答题(共66分)
-
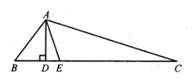
17. 已知甲、乙两人在同一地点出发，甲往东走了5km，乙往南走了3km．画出图形并求这时甲、乙两人间的距离。18. 如图，AD是△ABC的高线，AE是角平分线，若∠BAC：∠B：∠C=6：3：1，求∠DAE的度数。
19. 已知x>y，比较下列式子的大小，并说明理由。(1)、2x+1>2y+1；(2)、5-2x<5-2y20. 已知：如图，在△ABC中，D是BC上的点，AD=AB，E，F分别是AC，BD的中点，AC=6．求EF的长。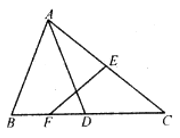
21. 已知，如图，点A、D、B、E在同一直线上，AC=EF，AD=BE，∠A=∠E，
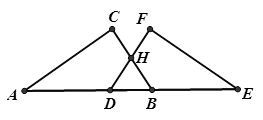(1)、求证：△ABC≌△EDF；(2)、当∠CHD=120°，猜想△HDB的形状，并说明理由．22. 已知：如图∠BAC的角平分线与BC的垂直平分线交于点D，DE⊥AB，DF⊥AC，垂足分别为点E，F。
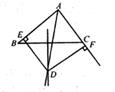(1)、求证：BE=CF。(2)、如果AB=10，AC=8，求BE的长。23. 如图，AD∥BC，∠BAD=90°，以点B为圆心，BC长为半径画弧，与射线AD相交于点E，连结BE，过C点作CF⊥BE，垂足为F。
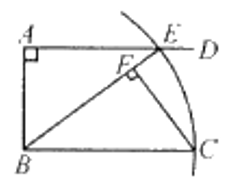(1)、线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上，然后再加以证明。结论：BF=。
证明：(2)、若AB=6，AE=8，求点A到点C的距离。24. 已知，在△ABC中，∠A=90°，AB=AC，点D为BC的中点。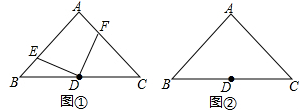
(1)、如图①，若点E、F分别为AB、AC上的点，且DE⊥DF。①求证：BE=AF；
②若S△BDE= S△ABC=2，求S△CDF；
(2)、若点E、F分别为AB、CA延长线上的点，且DE⊥DF。①BE=AF还成立吗?请利用图②说明理由。
②若S△BDE= S△ABC=8，直接写出DF的长。