浙江省Q21联盟2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 改革开放以来，我国众多科技实体在各自行业取得了举世瞩目的成就，大疆科技、华为集团、太极股份和凤凰光学等就是其中的杰出代表．上述四个企业的标志是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 以下列长度的三条线段为边，能构成三角形的是（）

A、7，8，15 B、15，20，4 C、7，6，18 D、6，7，5

查看试题解析
3. 已知a＜b，下列不等式中正确的是（）

A、 $\frac{a}{3} > \frac{b}{3}$ B、a﹣3＜b﹣3 C、a+3＞b+3 D、﹣3a＜﹣3b

查看试题解析
4. 下列语句是命题的是（）

A、作直线AB的垂线 B、在线段AB上取点C C、同旁内角互补 D、垂线段最短吗？

查看试题解析
5. 若一个三角形三个内角度数的比为2︰3︰5，那么这个三角形是（）

A、直角三角形 B、锐角三角形 C、钝角三角形 D、不能确定

查看试题解析
6. 如图，△ ABC和△ DEF中，AB=DE，角∠B=∠DEF，添加下列哪一个条件无法证明△ ABC≌△ DEF（）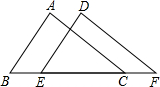

A、AC∥DF B、∠A=∠D C、∠ACB=∠F D、AC=DF

查看试题解析
7. 下列四种基本尺规作图分别表示：①作一个角等于已知角；②作一个角的平分线；③作一条线段的垂直平分线；④过直线外一点P作已知直线的垂线。则对应作法错误的是（）

A、① B、② C、③ D、④

查看试题解析
8. 如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A=36°，则∠DCB的度数为（）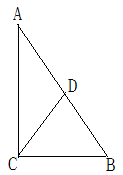

A、54° B、64° C、72° D、75°

查看试题解析
9. 如图所示，△ABC的顶点A，B，C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（）

A、3 B、2 C、4 D、1.5

查看试题解析
10. 如图，等边△ABC的边长为6，AD是BC边上的中线，M是AD上的动点，E是边AC上一点，若AE=2，则EM+CM的最小值为（）

A、 $\sqrt{26}$ B、 $\sqrt{27}$ C、 $\sqrt{28}$ D、 $\sqrt{32}$

查看试题解析

二、填空题（每题3分，共6小题，共18分）

11. 已知x与6的差大于2，用不等式表示为.

查看试题解析
12. 一个三角形的三边为2、5、x ，另一个三角形的三边为y、2、6，若这两个三角形全等，则x+y= .

查看试题解析
13. 已知等腰三角形的一个外角为108°，则其底角的度数为

查看试题解析
14. 公元3世纪初，中国古代数学家赵爽注《周髀算经》时，创造了“赵爽弦图”．如图，设勾 $a = 6$ ，弦 $c = 10$ ，则小正方形ABCD的面积是.

查看试题解析
15. 直线 $l_{1}$ ∥ $l_{2}$ ∥ $l_{3}$ ，且 $l_{1}$ 与 $l_{2}$ 的距离为1， $l_{2}$ 与 $l_{3}$ 的距离为3．把一块含有45°角的直角三角板如图放置，顶点A，B，C恰好分别落在三条直线上，则△ABC的面积为．

查看试题解析
16. 如图，△ABC中，已知∠C＝90°，∠B＝55°，点D在边BC上，BD＝2CD ．把△ABC绕着点D逆时针旋转m (0＜m＜180)度后，如果点B恰好落在初始Rt△ABC的边上，那么m的值为．

查看试题解析

三、解答题（共7小题，共52分）

17. 在如图所示的网格中，每个小正方形的边长均为1个单位．

(1)、请你在图1中画一个以格点为顶点，面积为6个平方单位的等腰三角形；

(2)、请你在图2中画一条以格点为端点，腰长为 $\sqrt{5}$ 的等腰三角形；

查看试题解析
18. 如图：已知D、E分别在AB、AC上，AB=AC，∠B=∠C，求证：BE=CD．

查看试题解析
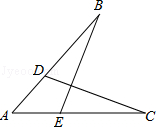19. 如图所示的一块地，∠ADC＝90°，AD＝12m，CD＝9m，AB＝25m，BC＝20m，求这块地的面积.

查看试题解析
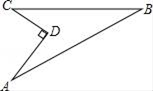20. 在△ABC中，AB=15，BC=14，AC=13，求△ABC的面积．某学习小组经过合作交流，给出了解题思路。

查看试题解析
21. 如图，△ABC中，AB＝BC，∠ABC＝90°，F为AB延长线上一点，点E在BC上，且AE＝CF．

(1)、求证：△ABE≌△CBF；

(2)、若∠CAE＝25°，求∠ACF的度数．

查看试题解析
22. 如图，△ABC中，AD⊥BC于点D，AD＝4cm，BD=3cm，△ABC的面积14 ${cm}^{2}$ ，动点P沿射线AD匀速运动，连结PB.

(1)、求DC的长；

(2)、若P的运动速度为2cm/s，当△ABP为等腰三角形时，求P点的运动时间t的值。

查看试题解析
23. 如图

(1)、如图①，AD是△ABC的中线.△ABD与△ACD的面积的数量关系是

(2)、例：若三角形的面积记为S，例如：△ABC的面积记为S△ABC.如图②，已知S△ABC＝1，△ABC的中线AD、CE相交于点O，求四边形BDOE的面积.
小华利用(1)的结论，解决了上述问题，解法如下：
连接BO，设S△BEO＝x，S△BDO＝y，由(1)结论可得：S△BCE＝S△BAD＝ $\frac{1}{2}$ S△ABC＝ $\frac{1}{2}$ ，
S△BCO＝2S△BDO＝2y，S△BAO＝2S△BEO＝2x.则有 ${\begin{matrix} S_{△ B E O} + S_{△ B C O} = S_{△ B C E} \\ S_{△ B A O} + S_{A B D O} = S_{△ B A D} \end{matrix}$ 即 ${\begin{matrix} x + 2 y = \frac{1}{2} \\ 2 x + y = \frac{1}{2} \end{matrix}$
所以x＋y＝ $\frac{1}{3}$ .即四边形BDOE面积为 $\frac{1}{3}$ .
请仿照上面的方法，解决下列问题：
如图③，已知S△ABC＝1，D、E是BC边上的三等分点，F、G是AB边上的三等分点，AD、CF交于点O，求四边形BDOF的面积.

(3)、如图④，已知S△ABC＝1，D、E、F是BC边上的四等分点，G、H、I是AB边上的四等分点，AD、CG交于点O，则四边形BDOG的面积为.

查看试题解析