云南省保山市2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-05 类型：期中考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 要使四边形木架（用四根木条钉成）不变形，至少要再钉上的木条的根数为（ ）
A、一条 B、两条 C、三条 D、零条3. 等腰三角形的一边长等于4，一边长等于9，则它的周长是（ ）A、17 B、22 C、17或22 D、134. 如图，在△ABC中，AD是BC边上的高，BE平分∠ABC交AC边于E，∠BAC=60°，∠ABE=25°，则∠DAC的大小是 （ ）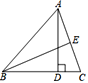
A、15° B、30° C、25° D、20°5. 如图，AB∥DC，AB=DC，要使△ABD≌△CDB，直接利用三角形全等的判定方法是（ ）
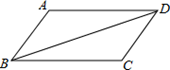A、AAS B、SAS C、ASA D、SSS6. 如图，一棵树在一次强台风中，从离地面5m处折断，倒下的部分与地面成30°角，这棵树在折断前的高度是（ ）
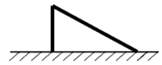A、5m B、10m C、15m D、20m7. 正九边形的一个内角的度数是（ ）A、108° B、120° C、135° D、140°8. 如图，△ABC的三边AB、BC、CA分别长为20、30、40，AO、BO、CO分别是三个内角平分线，则S△AOB：S△BOC：S△AOC等于（ ）
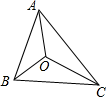A、1：1：1 B、1：2：3 C、2：3：4 D、3：4：5二、填空题
-
9. 点A（1，﹣3）关于x轴的对称点A′的坐标是.10. 如图，△ABC≌△DCB，若AC＝7，BE＝5，则DE的长为.
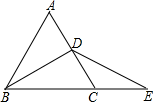
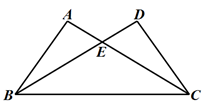11. 如图，点N是△ABC的AB边的延长线上一点，∠NAC=42°，∠NBC=84°，则∠C的大小=（度）．
12. 如图， AB的垂直平分线MN交AB于点M，交AC于点D，若∠A=38°，则∠BDM=度.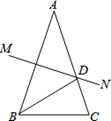
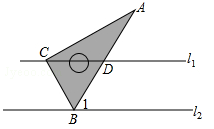
13. 如图，AD是等边三角形ABC的中线，AE=AD，则∠EDC=.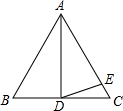
14. 含角30°的直角三角板与直线 ， 的位置关系如图所示，已知 ，∠1=60°，以下三个结论中正确的是（只填序号）。①AC=2BC ②△BCD为正三角形 ③AD=BD
三、解答题
-
15. 已知n边形的内角和θ=（n-2）×180°.(1)、当θ=720°时，求出边数n.(2)、小明说，θ能取820°，这种的说法对吗？若对，求出边数n；若不对，说明理由.16. 如图，在正方形网格中，每个小正方形的边长都是1，每个小正方形的顶点叫做格点．网格中有一个格点△ABC（即三角形的顶点都在格点上）．
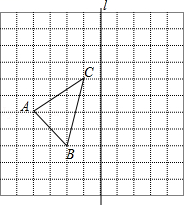
①在图中作出△ABC关于直线l对称的△A1B1C1 （要求A与A1 ， B与B1 ， C与C1相对应）；
②求△ABC的面积；
③在直线l上找一点P，使得△PAC的周长最小．
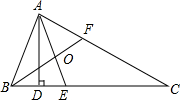
17. 如图，在△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠BAC=80°，∠ABC=70°.求∠BAD，∠AOF的度数.
18. 如图，点E、F在BC上，BE=CF，∠A=∠D，∠B=∠C，AF与DE交于点O.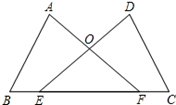
(1)、求证：∠AFB=∠DEC；(2)、若∠EOF=60°，试判断△OEF的形状，并说明理由.19. 如图，在△ABC中，AD是∠BAC的平分线，DE⊥AB、DF⊥AC，垂足分别为E、F，且BE=CF.求证：BD=CD.
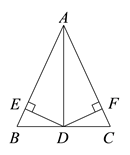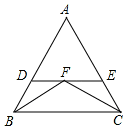
20. 如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E.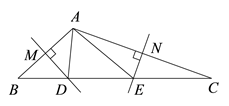
(1)、若BC=5，求△ADE的周长.(2)、若∠BAD+∠CAE=60°，求∠BAC的度数.21. 如图，在△ABC中，∠ABC的平分线BF与∠ACB的平分线CF相交于F，过点F作DE∥BC，交直线AB于点D，交直线AC于点E.求证：BD+CE=DE.
