江苏省无锡市宜兴市丁蜀学区2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入出卷网下载

一、单选题

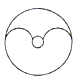
1. 下列图形中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若等腰三角形的两边长为3和7，则该等腰三角形的周长为（　　）

A、10 B、13 C、17 D、13或17

查看试题解析
3. 下列各组数中，不能作为直角三角形三边长度的是（）

A、2、3、4 B、3、4、5 C、6、8、10 D、5、12、13

查看试题解析
4. 某同学把一块三角形的玻璃打碎成了3块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事方法是（）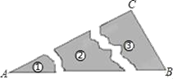

A、带①去 B、带②去 C、带③去 D、带①和②去

查看试题解析
5. 如图，点E，F在AC上，AD=BC，DF=BE，要使△ADF≌△CBE，还需要添加一个条件是（）

A、AD∥BC B、DF∥BE C、∠A=∠C D、∠D=∠B

查看试题解析
6. 如图的2×4的正方形网格中，△ABC的顶点都在小正方形的格点上，这样的三角形称为格点三角形，在网格中与△ABC成轴对称的格点三角形一共有（）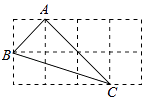

A、2个 B、3个 C、4个 D、5个

查看试题解析
7. 如图，△ABC中，AB=5，AC=8，BD，CD分别平分∠ABC，∠ACB，过点D作直线平行于BC，分别交AB，AC于E，F，则△AEF的周长为（）

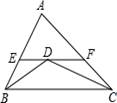A、12 B、13 C、14 D、18

查看试题解析
8. 到三角形的三个顶点距离相等的点是（）

A、三条角平分线的交点 B、三条中线的交点 C、三条高的交点 D、三条边的垂直平分线的交点

查看试题解析
9. 下列说法：①等腰三角形的两底角相等；②角的对称轴是它的角平分线；③成轴对称的两个图形中，对应点的连线被对称轴垂直平分；④全等三角形的对应边上的高相等；⑤在直角三角形中，如果有一条直角边长等于斜边长的一半.那么这条直角边所对的角等于30°.以上结论正确的个数（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，点P、Q分别是边长为4cm的等边△ABC边AB，BC上的动点，点P从顶点A，点Q从顶点B同时出发，且速度都为1cm/s，连接AQ、CP交于点M，下面四个结论：①BP＝CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第 $\frac{4}{3}$ 秒或第 $\frac{8}{3}$ 秒时，△PBQ为直角三角形，正确的有几个（）

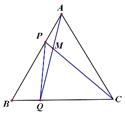A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 一个汽车牌照在水中的倒影为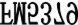，则该汽车牌照号码为.

查看试题解析
12. 一直角三角形的两条直角边长分别为12、5，则斜边上的中线长是

查看试题解析
13. 如图，△ABC≌△ADE，∠EAC＝35°，则∠BAD＝°.

查看试题解析
14. 如图，∠C＝90°，∠1＝∠2，若BC＝20，BD＝15，则点D到AB的距离为.

查看试题解析
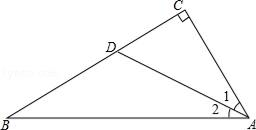15. 等腰三角形有一个角为70°，则底角的度数为.

查看试题解析
16. 如图，已知所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大正方形的边长为5，则A，B，C，D四个小正方形的面积之和等于 .

查看试题解析
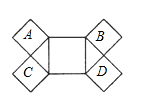17. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为40和28，则△EDF的面积为。

查看试题解析
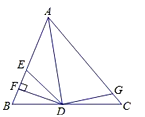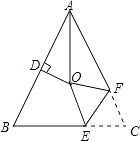
18.
如图，△ABC中，AB=AC，∠BAC=54°，∠BAC的平分线与AB的垂直平分线交于点O，将∠C沿EF（E在BC上，F在AC上）折叠，点C与点O恰好重合，则∠OEC为度．

查看试题解析

三、解答题

19. 已知：如图，BC∥EF，AD=BE，BC=EF，

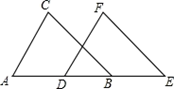
求证：

(1)、△ABC≌△DEF.

(2)、AC∥DF.

查看试题解析
20. 如图，∠A=∠B，AE=BE，点D在AC边上，∠1=∠2，AE和BD相交于点O.

(1)、求证：△AEC≌△BED；

(2)、若∠1=40°，求∠BDE的度数.

查看试题解析
21. 如图，在△ABC中，AB=AC，AC的垂直平分线分别交AB、AC于点D、E.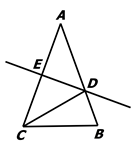

(1)、若∠A = 40°，求∠DCB的度数.

(2)、若AE=4，△DCB的周长为14，求△ABC的周长.

查看试题解析
22. 如图，小明所在学校的旗杆BD高约为13米，距离旗杆20米处刚好有一棵高约为3米的香樟树AE ．活动课上，小明有意在旗杆与香樟树之间的连线上来回踱步，发现有一个位置C到旗杆顶部与树顶的距离相等．请你求位置C与旗杆之间的距离.

查看试题解析
23. 如图，在8×8的正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.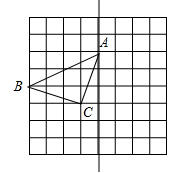

(1)、在图中作出△ABC关于直线l对称的△A₁B₁C₁；（要求：A与A₁ ， B与B₁ ， C与C₁相对应）

(2)、 $Δ A B C$ 是三角形；

(3)、若有一格点P到点A、B的距离相等（PA=PB），则网格中满足条件的点P共有个；

(4)、在直线 $l$ 上找一点Q，使QB+QC的值最小。

查看试题解析
24. 如图，已知点D为OB上的一点，请用直尺和圆规按下列要求进行作图，保留作图痕迹．

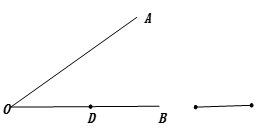(1)、作∠AOB的平分线OC；

(2)、在OC上取一点P，使得OP=a ；

(3)、爱动脑筋的小刚经过仔细观察后，进行如下操作：在边OA上取一点E，使得PE＝PD，这时他发现∠OEP与∠ODP之间存在一定的数量关系，请写出∠OEP与∠ODP的数量关系，并说明理由．

查看试题解析
25. 如图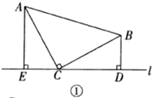

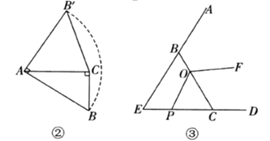(1)、观察推理：如图①，在 $Δ A B C$ 中， $∠ A C B = 90 ° ， A C = B C$ ，直线 $l$ 过点 $C$ ，点 $A ， B$ 在直线 $l$ 的同侧， $B D ⊥ l ， A E ⊥ l$ ，垂足分别为 $D ， E$ .求证： $Δ A E C ≅ Δ C D B$ .

(2)、类比探究：如图②，在 $R t Δ A B C$ 中， $∠ A C B = 90 ° ， A C = 4$ ，将斜边 $A B$ 绕点 $A$ 逆时针旋转90°至 $A B^{'}$ ，连接 $B^{'} C$ ，求 $Δ A B^{'} C$ 的面积.

(3)、拓展提升：如图③，在 $Δ E B C$ 中， $∠ E = ∠ E C B = 60 ° ， E C = B C = 3$ ，点 $O$ 在 $B C$ 上，且 $O C = 2$ ，动点 $P$ 从点 $E$ 沿射线 $E C$ 以每秒1个单位长度的速度运动，连接 $O P$ ，将线段 $O P$ 绕点 $O$ 逆时针旋转120°得到线段 $O F$ .要使点 $F$ 恰好落在射线 $E B$ 上，求点 $P$ 运动的时间 $t$ .

查看试题解析
26. 如图，已知△ABC中，∠B=90°，AB=16cm，BC=12cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．

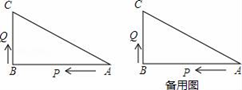(1)、出发2秒后，求PQ的长；

(2)、当点Q在边BC上运动时，出发几秒钟后，△PQB能形成等腰三角形？

(3)、当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析