江苏省无锡市锡北片2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入 出卷网 下载

一、单选题

  • 1. 下列美丽的图案中不是轴对称图形是（     ）
    A、 B、 C、 D、

    查看试题解析

  • 2. 在 227 ，-1.732. π2 . 93 .0.121121112…（每两个2中逐次多一个1）.- 0.01 中，无理数的个数是（ ）
    A、2个 B、3个 C、4个 D、5个

    查看试题解析

  • 3. 与数轴上的点一一对应的数是（  ）
    A、分数 B、有理数 C、无理数 D、实数

    查看试题解析

  • 4. 下列各组数中不能作为直角三角形的三边长的是（   ）
    A、6，12，8 B、7，24，25 C、1.5，2，2.5 D、9，12，15

    查看试题解析

  • 5. 有一块三角形的草坪△ABC，现要在草坪上建一座凉亭供大家休息，要使凉亭到草坪三条边的距离相等，则凉亭的位置应选在 （ ）
    A、△ABC三条角平分线的交点 B、△ABC三边的垂直平分线的交点 C、△ABC三条中线的交点 D、△ABC三条高所在直线的交点

    查看试题解析

  • 6. 若等腰三角形的两边长为3和4，则这个三角形的周长为（    ）
    A、10 B、11 C、12 D、10或11

    查看试题解析

  • 7. 如图，AC=DF，∠1=∠2，如果根据“ASA”判定△ABC≌△DEF，那么需要补充的条件是（   ）

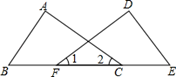    A、∠A=∠D B、AB=DE C、∠A=∠E D、∠B=∠E

    查看试题解析

  • 8. 如图，一个梯子AB长2.5米，顶端A靠在墙AC上，这时梯子下端B与墙角C距离为1.5米，梯子滑动后停在DE的位置上，测得BD长为0.9米，则梯子顶端A下落了（   ）

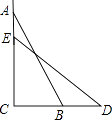    A、0.9米 B、1.3米 C、1.5米 D、2米

    查看试题解析

  • 9. 如图，已知Rt△ABC中，∠C＝90º，∠A＝30º，在直线BC或AC上取一点P，使得△PAB是等腰三角形，则符合条件的P点有（    ）

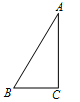    A、5个 B、6个 C、7个 D、8个

    查看试题解析

  • 10. 已知：如图在△ABC，△ADE中，∠BAC=∠DAE=90°，AB=AC，AD=AE，点C，D，E三点在同一条直线上，连接BD，BE．以下四个结论：①BD=CE；②BD⊥CE；③∠ACE+∠DBC=45°；④BE2=2（AD2+AB2），其中结论正确的个数是（   ）

    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题

  • 11.    16的算术平方根的平方根是.

    查看试题解析

  • 12. 小明从镜子中看到对面电子钟如图所示，这时的时刻应是.

    查看试题解析

  • 13. 已知△ABC≌△DEF，∠A=30°，∠B=80°，则∠F=.

    查看试题解析

  • 14. 等腰三角形的一个角是110°，则它的底角是 ．

    查看试题解析

  • 15. 已知|a-1|+ b+7 =0,则a+b=.

    查看试题解析

  • 16. 已知：如图，在△AOB中，∠AOB=90°，AO=3cm，BO=4cm．将△AOB绕顶点O，按顺时针方向旋转到△A1OB1处，此时线段OB1与AB的交点D恰好为AB的中点，则线段B1D=cm．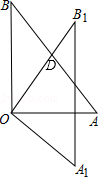

    查看试题解析

  • 17. 如图，已知AE平分∠BAC，BE⊥AE于E，ED∥AC，∠BAE=36°，则∠BED的度数为

    查看试题解析

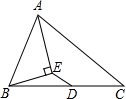  • 18. 如图，在Rt△ABC中，∠ACB=90°，∠ABC=60°，AB=4，点D是BC上一动点，以BD为边在BC的右侧作等边△BDE，F是DE的中点，连结AF，CF，则AF+CF的最小值是.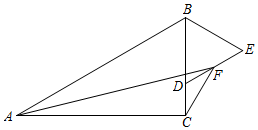

    查看试题解析

三、解答题

  • 19. 计算：
    (1)、−(−1)−|2−2|+(π−3.14)0     
    (2)、16+−273+(−2)2

    查看试题解析

  • 20. 解方程：
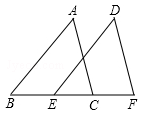
    (1)、2x3+16=0
    (2)、(x+1)−24=0

    查看试题解析

  • 21. 如图，已知点B、E、C、F在同一条直线上，AB=DE，∠A=∠D，AC∥DF.求证：BE=CF.

    查看试题解析

  • 22. 如图，△ABC中，AB=AC=5，线段AB的垂直平分线DE分别交边AB、AC于点E、D.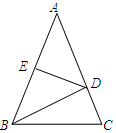

    (1)、若∠A=40°，求∠DBC的度数；
    (2)、若△BCD的周长为8，求BC的长.

    查看试题解析

  • 23. 如图，四边形ABCD中，∠ABC＝90°，AB＝4，BC＝3，CD＝12， AD＝13.求四边形ABCD的面积.

    查看试题解析

  • 24. 利用网格线作图：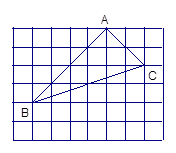

    (1)、在BC上找一点P，使点P到AB和AC的距离相等；
    (2)、在射线AP上找一点Q，使QB=QC.

    查看试题解析

  • 25. 如图，△ABC中，AB=BC，BE⊥AC于点E，AD⊥BC于点D，∠BAD=45°，AD与BE交于点F，连接CF.

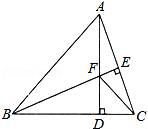    (1)、求证：BF=2AE；
    (2)、若CD=1，求AD的长.

    查看试题解析

  • 26. 【问题】

    如图1，在Rt△ABC中，∠ACB=90°，AC=BC，过点C作直线l平行于AB.∠EDF=90°，点D在直线l上移动，角的一边DE始终经过点B，另一边DF与AC交于点P，研究DP和DB的数量关系.

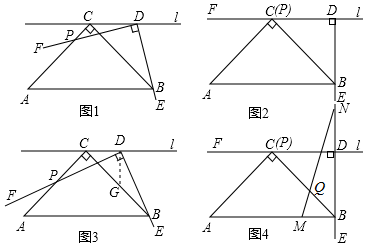    (1)、【探究发现】如图2，某数学兴趣小组运用“从特殊到一般”的数学思想，发现当点D移动到使点P与点C重合时，通过推理就可以得到DP=DB，请写出证明过程；
    (2)、【数学思考】如图3，若点P是AC上的任意一点（不含端点A、C），受（1）的启发，这个小组过点D作DG⊥CD交BC于点G，就可以证明DP=DB，请完成证明过程；
    (3)、【拓展引申】如图4，在（1）的条件下，M是AB边上任意一点（不含端点A、B），N是射线BD上一点，且AM=BN，连接MN与BC交于点Q，这个数学兴趣小组经过多次取M点反复进行实验，发现点M在某一位置时BQ的值最大.若AC=BC=4，请你直接写出BQ的最大值.

    查看试题解析

  • 27. 如图，△ABC中，∠ACB=90°，AB=5cm，BC=3cm，若点P从点A出发，以每秒2cm的速度沿折线A-C-B-A运动，设运动时间为t秒（t＞0）．

    (1)、若点P在AC上，且满足PA=PB时，求出此时t的值；
    (2)、若点P恰好在∠BAC的角平分线上，求t的值；
    (3)、在运动过程中，直接写出当t为何值时，△BCP为等腰三角形．

    查看试题解析