江苏省南通市海安市八校联考2019-2020学年八年级上学期数学期中考试试卷

试卷更新日期：2019-12-05 类型：期中考试

进入出卷网下载

一、单选题

1. 已知三角形的两边长分别为3和4，则第三边长x的范围是（）

A、3<x<4 B、1<x<7 C、1<x<5 D、无法确定

查看试题解析
2. 计算 ${(- x)}^{3} \cdot x^{2}$ 的结果是（）

A、 $x^{5}$ B、 $- x^{5}$ C、 $x^{6}$ D、 $- x^{6}$

查看试题解析
3. 点P(a，b)与点Q（-2，-3）关于x轴对称，则a+b=（）

A、-5 B、5 C、1 D、-1

查看试题解析
4. 已知图中的两个三角形全等，则∠1等于（）

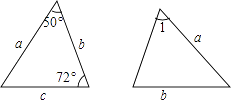A、50° B、58° C、60° D、72°

查看试题解析
5. 如图，在△ABC中，BC的垂直平分线分别交AC，BC于点D，E.若△ABC的周长为24，CE＝4，则△ABD的周长为（）

A、16 B、18 C、20 D、24

查看试题解析
6. 下列两个多项式相乘，不能用平方差公式的是（）

A、(-5a+2b)(5a+2b) B、(-5a+2b)(-5a-2b) C、(-5a-2b)(5a-2b) D、(5a+2b)(-5a-2b)

查看试题解析
7. 用一条长为18cm的细绳围成一个等腰三角形，若其中有一边的长为5cm，则该等腰三角形的腰长为（）cm

A、5 B、6.5 C、5或6.5 D、6.5或8

查看试题解析
8. 在直角坐标系中，已知A（3，3），在x轴、y轴上确定一点P，使△AOP为等腰三角形，则符合条件的点P共有（）

A、4个 B、7个 C、8个 D、10个

查看试题解析
9. 如图，OP平分∠AOB，PA⊥OA、PB⊥OB，垂足分别为A、B，下列结论成立的是（）

①PA=PB；②PO平分∠APB；③OA=OB；④AB垂直平分OP

A、①③ B、①②③ C、②③ D、①②③④

查看试题解析
10. 古希腊数学家把数1，3，6，10，15，21，…叫做三角形数，其中1是第1个三角形数，3是第2个三角形数，6是第3个三角形数，…，依此类推，那么第11个三角形数是多少，2016是第几个三角形数，则选（）

A、55，63 B、66，63 C、55，64 D、66，64

查看试题解析

二、填空题

11. 一个多边形的内角和等于一个三角形的外角和的2倍，则这个多边形的边数是.

查看试题解析
12. 若 $3^{x} = 5$ ， $3^{y} = 15$ ，则 $3^{x - y}$ =.

查看试题解析
13. 如果(x－2)(x＋3)＝x²＋px＋q，那么p＋q的值为.

查看试题解析
14. 如果9x²-axy+4y²是完全平方式，则a的值是.

查看试题解析
15. 如图，在ΔABC中，AD⊥BC，AE平分∠BAC，若∠1=40°，∠2=25°，则∠B=.

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，∠B=30°，CD是斜边AB上的高，AD=3，则线段BD的长为.

查看试题解析
17. a，b，c为ΔABC的三边，化简|a-b-c|-|a+b-c|+2a结果是.

查看试题解析
18. 如图，在正方形ABCD中，AB=2，延长BC到点E，使CE=1，连接DE，动点P从点A出发以每秒1个单位的速度沿AB-BC-CD-DA向终点A运动，设点P的运动时间为t秒，当△ABP和△DCE全等时，t的值.

查看试题解析

三、解答题

19. 计算或化简：

(1)、 $4^{2018} \times {(- 0.25)}^{2019}$

(2)、 ${(2 x + y - 1)}^{2}$

(3)、 $(3 x + 4) (3 x - 4) - (2 x + 3) (3 x - 2)$

(4)、 $(0.25 a^{2} b - \frac{1}{2} a^{3} b^{2} - \frac{1}{6} a^{4} b^{3}) \div (0.5 a^{2} b)$

查看试题解析
20. 如图所示，在平面直角坐标系中，A（-1，5）、B（-1，0）、C（-3，6）.

(1)、直接写出△ABC 的面积；

(2)、在图形中作出△ABC 关于x轴的对称图形△A₁B₁C₁ ，并直接写出△A₁B₁C₁的三个顶点的坐标：A₁（），B₁（），C₁（）.

查看试题解析
21. 如图，已知△ABC，∠C = 90°， $A C < B C$ .D为BC上一点，且到A，B两点的距离相等.

(1)、用直尺和圆规，作出点D的位置（不写作法，保留作图痕迹）；

(2)、连结AD，若∠B = 35°，求∠CAD的度数.

查看试题解析
22. 已知：如图，AB=AC，PB=PC，PD⊥AB，PE⊥AC，垂足分别为D、E.证明：PD=PE.

查看试题解析
23. 如图1，已知 $Δ A B C$ 中，点 $D$ 在 $A B$ 边上， $D E ∥ B C$ 交边 $A C$ 于点 $E$ ，且 $D E$ 平分 $∠ A D C$ .

(1)、求证： $D B = D C$ ；

(2)、如图2，在 $B C$ 边上取点 $F$ ，使 $∠ D F C = 60^{°}$ ，若 $B C = 7$ ， $B F = 2$ ，求 $D F$ 的长。

查看试题解析
24.

(1)、已知 $a (a + 1) - (a^{2} + 2 b) = 1$ ，求 ${(a - 2 b)}^{2} - 2 a + 4 b$ 的值.

(2)、若 ${(a + 2)}^{0}$ 无意义，且 $2 a + 5 b = 0$ 先化简再求 $[(a + 4 b) (a - 4 b) - {(a - 2 b)}^{2}] \div 4 b$ 的值.

查看试题解析
25. 如图，△ABC是边长为5cm的等边三角形，点P，Q分别从顶点A，B同时出发，沿线段AB，BC运动，且它们的速度都为1cm/s.当点P到达点B时，P，Q两点停止运动，设点P的运动时间为t（s）.

(1)、当t为何值时，△PBQ是直角三角形？

(2)、连接AQ、CP，相交于点M，则点P，Q在运动的过程中，∠CMQ会变化吗？若变化，则说明理由；若不变，请求出它的度数.

查看试题解析
26. 如图，在平面直角坐标系中， $A (8 ， 0)$ ，点 $B$ 在第一象限， $Δ O A B$ 为等边三角形， $O C ⊥$ $A B$ ，垂足为点 $C$ . $C F ⊥$ $O A$ ，垂足为 $F$ .

(1)、求OF的长；

(2)、作点 $C$ 关于 $y$ 轴的对称点 $D$ ，连 $D A$ 交 $O B$ 于E，求OE的长.

查看试题解析