江苏省连云港市海州区四校2019-2020学年八年级上学期数学期中考试试卷
试卷更新日期：2019-12-05 类型：期中考试
一、单选题
-
1. 下列图形中，不是轴对称图形的是（ ）A、
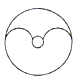B、
C、
D、
2. 下列给出的三条线段的长，能组成直角三角形的是（ ）A、1 、 2 、3 B、2 、 3、 4 C、5、 7 、 9 D、6、 8、 103. 一个等腰三角形两边的长分别为4和9，那么这个三角形的周长是（ ）A、13 B、17 C、22 D、17或224. 如图，下列条件中，不能证明△ABD≌△ACD的是（ ）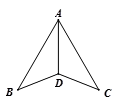
A、AB＝AC ，BD＝CD B、∠B＝∠C，∠BAD＝∠CAD C、∠B＝∠C，BD＝CD D、∠ADB＝∠ADC，DB＝DC5. 如图，用直尺和圆规作一个角的平分线，是运用了“全等三角形对应角相等”这一性质，由作图所得条件，判定三角形全等运用的方法是（ ）
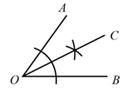A、SAS B、ASA C、AAS D、SSS6. 如图，在△ABC中，AB=AC，D为BC中点，∠BAD=20°， 则∠C的度数是（ ）
A、20 ° B、45° C、60° D、70°7. 如图，在△ABC中，CE平分∠ACB，CF平分∠ACD，且EF∥BC交AC于M，若CM＝3，则CE2+CF2的值为（ ）
A、6 B、9 C、18 D、368. 如图3，∠AOP=∠BOP=15°，PC∥OA，若PC=4，则PD等于（ ）
A、1 B、3 C、4 D、2二、填空题
-
9. 如图，若Rt△ABC≌Rt△ADE，且∠B=60°，则∠E=°
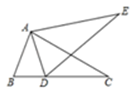10.如图，∠1=∠2，要使△ABD≌△ACD，需添加的一个条件是 （只添一个条件即可）．
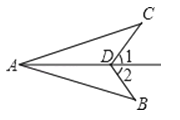11. 如图，将一根长12厘米的筷子置于底面直径为6厘米，高为8厘米的圆柱形杯子中，则筷子露在杯子外面的长度至少为厘米.
12. 如图，A、E、C三点在一条直线上，△ABE≌△CED，∠A=∠C=90°，AB=3cm，CD=7cm，则AC= cm.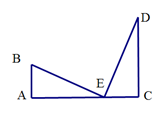
13. 如图，△ABC中，DE是AC的垂直平分线，AE=4cm，△ABD的周长为12cm，则△ABC的周长为cm.
14. 如图，△ABC≌△ADE，BC的延长线经过点E，交AD于F，∠ACB=∠AED=105°，∠CAD=10°，∠B=50°，则∠EAB= °.
15. 如图，△ABC为等边三角形，BD⊥AB，BD=AB，则∠DCB= .
16. 如图所示，在△ABC中，∠B=90°，AB=3，AC=5，将△ABC折叠，使点C与点A重合，折痕为DE，则△ABE的周长为.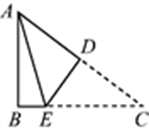
17. 如图，在△ABC 中，∠C=90°，∠A=34°，D，E 分别为 AB，AC 上一点，将△BCD，△ADE 沿 CD，DE 翻折，点 A，B 恰好重合于点 P 处，则∠ACP=.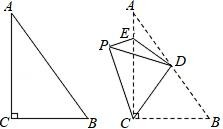
三、解答题
-
18. 如图，已知等边△ABC中，BD=CE，AD与BE相交于点P，求∠APE的度数.
19. 如图，在正方形网格中，每个小正方形的边长都为1，网格中有一个格点△ABC（即三角形的顶点都在格点上）.
(1)、△ABC的面积为；(2)、①在图中作出△ABC关于直线MN的对称图形△A′B′C′.②利用网格纸，在MN上找一点P，使得PB+PC的距离最短.( 保留痕迹)
20. 如图，已知AB=CD，AE⊥BD，CF⊥BD，垂足分别为E、F，BF=DE.求证：AB∥CD.
21. 如图，已知在AB、AC上各取一点E、D，使AE=AD，连结BD、CE相交于点O，连结AO，∠1=∠2，求证：∠B=∠C.
22. 如图，某学校（A点）与公路（直线L）的距离为300米，又与公路车站（D点）的距离为500米，现要在公路上建一个小商店（C点），使之与该校A及车站D的距离相等，求商店与车站之间的距离.
23. 如图，在△ABC中，AB＝AC，D为BC边上一点，∠B＝30°，∠DAB＝45°.
(1)、求∠DAC的度数；(2)、求证：DC＝AB.24. 已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F。
(1)、图中哪条线段和BE相等？为什么？(2)、若AB=6，AC=3，求BE的长。25. 如图，在△ACB中，∠ACB=90°，∠A=75°，点D是AB的中点.将△ACD沿CD翻折得到△A′CD，连接A′B.
(1)、求证：CD∥A′B；(2)、若AB=4，求A′B2的值.26. 如图(1)， ，.点P在线段AB上以 的速度由点A向点B运动，同时，点Q在线段BD上由点B向点D运动.它们运动的时间为 .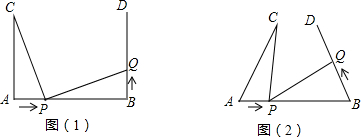
(1)、若点Q的运动速度与点P的运动速度相等，当 时， 与 是否全等，请说明理由，并判断此时线段PC和线段PQ的位置关系；(2)、如图(2)，将图(1)中的“ ，”为改“”，其他条件不变.设点Q的运动速度为 ，是否存在实数x，使得 与 全等？若存在，求出相应的x、t的值；若不存在，请说明理由.27. 如图
(1)、操作发现：如图1，D是等边三角形ABC边BA上一动点（点D与点B不重合），连接DC，以DC为边在BC上方作等边三角形DCF，连接AF.你能发现线段AF与BD之间的数量关系吗？并证明你发现的结论.(2)、类比猜想：如图2，当动点D运动到等边三角形ABC边BA的延长线上时，其他作法与（1）相同，猜想AF与BD在（1）中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明.(3)、深入探究：①如图3，当动点D在等边三角形ABC的边BA上运动时（点D与点B不重合），连接DC，以DC为边在其上方、下方分别作等边三角形DCF和等边三角形DCF'，连接AF，BF′.探究AF，BF′与AB有何数量关系？并证明你发现的结论。②如图4，当动点D在等边三角形ABC的边BA的延长线上运动时，其他作法与图3相同，①中的结论是否仍然成立？如果成立，请证明；如果不成立，是否有新的结论？如果有新的结论，直接写出新的结论，不需证明.