辽宁省鞍山市台安县2020届九年级上学期数学10月月考试卷

试卷更新日期：2019-12-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列函数解析式中，一定为二次函数的是（　　）

A、 $y = 3 x - 1$ B、y=ax²+bx+c C、 $s = 2 t^{2} - 2 t + 1$ D、 $y = x^{2} + \frac{1}{x}$

查看试题解析
2. 方程x²﹣3＝0的根是（）

A、 $\sqrt{3}$ B、﹣ $\sqrt{3}$ C、± $\sqrt{3}$ D、3

查看试题解析
3. 一元二次方程 $3 x^{2} - 4 x + 1 = 0$ 根的情况为（）

A、没有实数根 B、有两个不相等的实数根 C、有两个相等的实数根 D、只有一个实数根

查看试题解析
4. 下列关于函数 $y = - x^{2}$ 的图象及其性质的说法错误的是（）

A、开口向下 B、顶点是原点 C、对称轴是y轴 D、函数有最小值是0

查看试题解析
5. 若方程 2x²-3x+c=0 的一个根是 $\frac{1}{2}$ ，则 $c$ 的值是（）

A、 $\frac{3}{2}$ B、1 C、0 D、 $- \frac{1}{2}$

查看试题解析
6. 当ab＞0时，y＝ax²与y＝ax＋b的图象大致是（）

A、 B、 C、 D、

查看试题解析
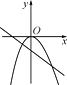7. 在元旦庆祝活动中，参加活动的同学互赠贺卡，共送贺卡90张，则参加活动的有（）人.

A、9 B、10 C、12 D、15

查看试题解析
8. 已知一个直角三角形的两条边的长恰好是方程 $x^{2} - 14 x + 48 = 0$ 的两个根，则这个直角三角形的第三边的长是（）

A、10 B、10或 $4 \sqrt{3}$ C、10或 $2 \sqrt{7}$ D、14

查看试题解析

二、填空题

9. 将一元二次方程 $- 2 x (x - 5) = 3 - x$ 化成一般形式（二次项系数是正数）为.

查看试题解析
10. 把方程 $x^{2} - 4 x + 1 = 0$ 配方变形为.

查看试题解析
11. 若抛物线 $y = (a - 3) x^{2}$ 开口向上，则 $a$ 的取值范围是.

查看试题解析
12. 已知关于 $x$ 的一元二次方程 $(a - 1) x^{2} - 4 x - 5 = 0$ 有实数根，则 $a$ 的取值范围是.

查看试题解析
13. 若点 $A (- 2, y_{1})$ 、 $B (- 1, y_{2})$ 、 $C (8, y_{3})$ 都在二次函数 $y = a x^{2} (a < 0)$ 的图象上，则 $y_{1}$ 、 $y_{2}$ 、 $y_{3}$ 从小到大的关系是.（用“ $<$ ”表示）.

查看试题解析
14. 有一人患了流感，经过两轮传染后共有81人患了流感，设每轮传染中一个人都传染了 $x$ 人，根据题意可列方程为.

查看试题解析
15. 如图，抛物线 $y = a x^{2}$ 与直线 $y = b x + c$ 的两个交点坐标分别为 $A (- 3 ， 4)$ ， $B (2 ， 1)$ ，则方程 $a x^{2} = b x + c$ 的解是.

查看试题解析
16. 已知一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ：
①若方程两根为-1和2，则 $2 a + c = 0$ ；②若 $b > a + c$ ，则一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根；③若 $b = 2 a + 3 c$ ，则一元二次方程 $a x^{2} + b x + c = 0$ 有两个不相等的实数根；④若 $m$ 是方程 $a x^{2} + b x + c = 0$ 的一个根，则一定有 $b^{2} - 4 a c = {(2 a m + b)}^{2}$ 成立.其中正确的是.

查看试题解析

三、解答题

17. 解方程：

(1)、 $3 x (2 x + 1) = 4 x + 2$

(2)、 $3 x^{2} - 6 x - 2 = 0$

查看试题解析
18. 关于x的一元二次方程x²＋（2m＋1）x＋m²－1=0有两个不相等的实数根.

(1)、求m的取值范围；

(2)、写出一个满足条件的m的值，并求此时方程的根.

查看试题解析
19. 如图所示，正方形 $E F G H$ 的顶点在边长为3的正方形 $A B C D$ 边上，设 $A F = x$ ，正方形 $E F G H$ 的面积为 $y$ .

(1)、求 $y$ 与 $x$ 之间的函数关系式，并写出自变量的取值范围；

(2)、若正方形 $E F G H$ 的面积为5，求 $A F$ 的长.

查看试题解析
20. 为响应国家全民阅读的号召，某社区鼓励居民到社区阅览室借阅读书，并统计每年的借阅人数和图书借阅总量（单位：本），该阅览室在2014年图书借阅总量是7500本，2016年图书借阅总量是10800本．

(1)、求该社区的图书借阅总量从2014年至2016年的年平均增长率；

(2)、已知2016年该社区居民借阅图书人数有1350人，预计2017年达到1440人，如果2016年至2017年图书借阅总量的增长率不低于2014年至2016年的年平均增长率，那么2017年的人均借阅量比2016年增长a%，求a的值至少是多少？

查看试题解析
21. 有座抛物线形拱桥（如图），正常水位时桥下河面宽 $20 m$ ，河面距拱顶 $4 m$ ，为了保证过往船只顺利航行，桥下水面的宽度不得小于 $18 m$ .

(1)、求出如图所示坐标系中的抛物线的解析式；

(2)、求水面在正常水位基础上上涨多少米时，就会影响过往船只航行？

查看试题解析
22. 对于一元二次方程 $a x^{2} + b x + c = 0 (a \neq 0)$ ，如果方程有两个实数根 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} = - \frac{b}{a}$ ， $x_{1} \cdot x_{2} = \frac{c}{a}$ （说明：定理成立的条件 $Δ \geq 0$ ）.例如方程 $2 x^{2} - 3 x - 1 = 0$ 中， $Δ = 17$ ，所以该方程有两个不等的实数解.设方程的两根为 $x_{1}$ ， $x_{2}$ ，那么 $x_{1} + x_{2} = \frac{3}{2}$ ， $x_{1} \cdot x_{2} = - \frac{1}{2}$ ，请根据上面阅读材料解答下列各题：

(1)、已知方程 $x^{2} - 3 x - 2 = 0$ 的两根为 $x_{1}$ 、 $x_{2}$ ，求 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值；

(2)、已知 $x_{1}$ ， $x_{2}$ 是一元二次方程 $4 k x^{2} - 4 k x + k + 1 = 0$ 的两个实数根，是否存在实数 $k$ ，使 $(2 x_{1} - x_{2}) (x_{1} - 2 x_{2}) = - \frac{3}{2}$ 成立？若存在，求出 $k$ 的值；若不存在，请说明理由.

查看试题解析
23. 一商店销售某种商品，平均每天可售出20件，每件盈利40元.为了扩大销售，增加盈利，该店采取了降价措施.在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件.

(1)、若降价 $a$ 元，则平均每天销售数量为件（用含 $a$ 的代数式表示）；

(2)、当每件商品降价多少元时，该商店每天销售利润为1050元？

查看试题解析
24. 某学校计划利用一片空地建一个学生自行车车棚，其中一面靠墙，这堵墙的长度为12米.计划建造车棚的面积为80平方米，已知现有的木板材料可使新建板墙的总长为26米.

(1)、为了方便学生出行，学校决定在与墙平行的一面开一个2米宽的门，那么这个车棚的长和宽分别应为多少米？

(2)、如图，为了方便学生取车，施工单位决定在车棚内修建几条等宽的小路，使得停放自行车的面积为54平方米，那么小路的宽为多少米？

查看试题解析
25. 如图①，在矩形 $A B C D$ 中， $A B = 8$ ， $A D = 4$ .点 $P$ 从点 $A$ 出发，沿 $A \to D \to C \to D$ 运动，速度为每秒2个单位长度；点 $Q$ 从点 $A$ 出发向点 $B$ 运动，速度为每秒1个单位长度. $P$ 、 $Q$ 两点同时出发，点 $Q$ 运动到点 $B$ 时，两点同时停止运动，设点 $Q$ 的运动时间为 $t$ （秒）.连结 $P Q$ 、 $A C$ 、 $C P$ 、 $C Q$ .

(1)、点 $P$ 到点 $C$ 时， $t =$ ；当点 $Q$ 到终点时， $P C$ 的长度为；

(2)、用含 $t$ 的代数式表示 $P D$ 的长；

(3)、当 $△ C P Q$ 的面积为9时，求 $t$ 的值.

查看试题解析
26. 如图，直线 $l$ 过 $x$ 轴上一点 $A (2 ， 0)$ ，且与抛物线 $y = a x^{2}$ 相交于 $B ， C$ 两点， $C$ 点坐标为 $(- 2 ， 4)$ .

(1)、求直线 $l$ 和抛物线的函数解析式.

(2)、若抛物线上有一点 $D$ 使得 $S_{△ A O D} = S_{△ O B C}$ ，求 $D$ 点坐标.

(3)、在 $x$ 轴上是否存在一点 $P$ ，使 $△ P O C$ 为等腰三角形？若存在，请直接写出点 $P$ 的坐标；若不存在，请说明理由.

查看试题解析