江苏省扬州市江都区邵樊片2020届九年级上学期数学第一次月考试卷

试卷更新日期：2019-12-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列方程中，关于x的一元二次方程是（）

A、3(x＋1)²＝2(x＋1) B、 $\frac{1}{x^{2}}$ ＋ $\frac{1}{x}$ －2＝0 C、ax²＋bx＋c＝0 D、x²＋2x＝x²－1

查看试题解析
2. 用配方法解方程 $x^{2} - 2 x - 1 = 0$ 时，配方后所得的方程为（）

A、 $（ x + 1 ）^{2} = 0$ B、 $（ x - 1 ）^{2} = 0$ C、 $（ x + 1 ）^{2} = 2$ D、 $（ x - 1 ）^{2} = 2$

查看试题解析
3. 一元二次方程 $x^{2} + x - 1 = 0$ 的根的情况为（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 已知x₁ ， x₂是一元二次方程x²﹣4x+1=0的两个实数根，则x₁•x₂等于（）

A、﹣4 B、﹣1 C、1 D、4

查看试题解析
5. 在数轴上，点 $A$ 所表示的实数为 $3$ ，点 $B$ 所表示的实数为 $a$ ， $⊙ A$ 的半径为 $2$ .那么下列说法中不正确的是（）

A、当 $a < 1$ 时，点 $B$ 在 $⊙ A$ 外 B、当 $1 < a < 5$ 时，点 $B$ 在 $⊙ A$ 内 C、当 $a < 5$ 时，点 $B$ 在 $⊙ A$ 内 D、当 $a > 5$ 时，点 $B$ 在 $⊙ A$ 外

查看试题解析
6. 如图，⊙O的半径是3，点P是弦AB延长线上的一点，连接OP，若OP＝4，∠APO＝30°，则弦AB的长为（）

A、2 $\sqrt{5}$ B、 $\sqrt{5}$ C、2 $\sqrt{13}$ D、 $\sqrt{13}$

查看试题解析
7. 若 $a$ ， $b$ 是方程 $x^{2} + 2 x - 2006 = 0$ 的两根，则 $a^{2} + 3 a + b = ($ $)$

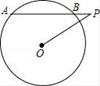A、 $2006$ B、 $2005$ C、 $2004$ D、 $2002$

查看试题解析
8. 如图，在平面直角坐标系xOy中，以原点O为圆心的圆过点A(13，0)直线y=kx-3k+4与交于B、C两点，则弦BC的长的最小值为（）

A、22 B、24 C、 D、

查看试题解析

二、填空题

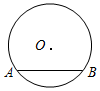
9. 请你写出一个有一根为1的一元二次方程：.

查看试题解析
10. 若关于x的一元二次方程（m﹣1）x²+x+m²﹣1＝0有一个根为0，则m的值为.

查看试题解析
11. 学校组织一次乒乓球赛，要求每两队之间都要赛一场.若共赛了15场，则有几个球队参赛？设有 $x$ 个球队参赛，列出正确的方程.

查看试题解析
12. 已知 $⊙ O$ 的半径为 $10 c m$ ， $A B$ ， $C D$ 是 $⊙ O$ 的两条弦， $A B / / C D$ ， $A B = 16 c m$ ， $C D = 12 c m$ ，则弦 $A B$ 和 $C D$ 之间的距离是 $c m$ ．

查看试题解析
13. 若关于 $x$ 的 $k x^{2} - 2 x - 1 = 0$ 有实数根，则 $k$ 的取值范围是.

查看试题解析
14. 某厂一月份生产某机器200台，计划二、三月份共生产1800台. 设二、三月份每月的平均增长率为 $x$ ，根据题意列出的方程是.

查看试题解析
15. 若 ${(a^{2} + b^{2})}^{2} - 3 (a^{2} + b^{2}) - 4 = 0$ ，则代数式 $a^{2} + b^{2}$ 的值为.

查看试题解析
16. 已知 $x^{2} + y^{2} + 4 x - 6 y + 13 = 0$ ，且x，y是实数，则x^y=.

查看试题解析
17. 如图，已知 $⊙ O$ 的半径为5，弦AB长度为8，则 $⊙ O$ 上到弦AB所在直线的距离为2的点有个 $.$

查看试题解析
18. 如图， $⊙ M$ 的半径为2，圆心 $M$ 的坐标为 $(3 ， 4)$ ，点 $P$ 是 $⊙ M$ 上的任意一点， $P A ⊥ P B$ ，且 $P A$ 、 $P B$ 与 $x$ 轴分别交于 $A$ 、 $B$ 两点，若点 $A$ 、 $B$ 关于原点 $O$ 对称，则 $A B$ 的最小值为.

查看试题解析

三、解答题

19. 解方程：
$(1) x (x + 4) = - 5 (x + 4)$ ；

查看试题解析
20. 先化简，再求值： $(\frac{x^{2}}{x - 1} - x + 1) \div \frac{4 x^{2} - 4 x + 1}{1 - x}$ ，其中x满足 $x^{2} + x - 2 = 0$ .

查看试题解析
21. 关于 $x$ 的一元二次方程 $(m - 2) x^{2} + 2 m x + m + 3 = 0$ 有两个不相等的实数根.

(1)、求 $m$ 的取值范围；

(2)、当 $m$ 取满足条件的最大整数时，求方程的根.

查看试题解析
22. 已知关于 $x$ 的一元二次方程 $x^{2} - (m - 1) x - 2 (m + 3) = 0$ .试证：无论 $m$ 取任何实数，方程都有两个不相等的实数根.

查看试题解析
23. 现代互联网技术的广泛应用，加速了快递行业的发展，据调查，某家小型快递公司，今年3月与5月完成投递的快件总数分别为10万件和14.4万件，现假定该公司每月投递的快件总数的增长率相同.

(1)、求该快递公司投递快件总数的月平均增长率？

(2)、如果该公司平均每名快件投递业务员每月最多可投递快件0.6万件，那么该公司现有的21名快件投递业务员能否完成今年6月的快件投递任务？如果不能，请问至少需要增加几名业务员？

查看试题解析
24. 如图， $⊙ O$ 的半径 $O D ⊥$ 弦 $A B$ 于点 $C$ ，连接 $A O$ 并延长交 $⊙ O$ 于点 $E$ ，连接 $E C$ ，已知 $A B = 8 ， C D = 2$ .

(1)、求 $O A$ 的长.

(2)、求 $C E$ 的长.

查看试题解析
25. 已知关于 $x$ 的方程 $x^{2} - (2 m + 1) x + m^{2} + m = 0$ .

(1)、用含 $m$ 的代数式表示这个方程的实数根.

(2)、若 $R t Δ A B C$ 的两边 $a 、 b$ 恰好是这个方程的两根，另一边长 $c = 5$ ，求 $m$ 的值.

查看试题解析
26. 如图， $A B$ 为半圆 $O$ 的直径，半径 $O P ⊥ A B$ ，过劣弧 $A P$ 上一点 $D$ 作 $D C ⊥ A B$ 于点 $C$ ，连接 $D B$ ，交 $O P$ 于点 $E$ ， $∠ D B A = 22.5 °$ .

(1)、若 $O C = 2$ ，则 $A C$ 的长为.

(2)、试写出 $A C$ 与 $P E$ 之间的数量关系，并说明理由.

查看试题解析
27. 如图1，一次函数y=﹣x+10的图象交x轴于点A，交y轴于点B.以P（1，0）为圆心的⊙P与y轴相切，若点P以每秒2个单位的速度沿x轴向右平移，同时⊙P的半径以每秒增加1个单位的速度不断变大，设运动时间为t（s）

(1)、点A的坐标为，点B的坐标为， ∠OAB=°；

(2)、在运动过程中，点P的坐标为， ⊙P的半径为（用含t的代数式表示）；

(3)、当⊙P与直线AB相交于点E、F时
①如图2，求t= $\frac{5}{2}$ 时，弦EF的长；

②在运动过程中，是否存在以点P为直角顶点的Rt△PEF，若存在，请求出t的值；若不存在，请说明理由（利用图1解题）.

查看试题解析