江苏省盐城市2020届九年级上学期数学第一次月考试卷
试卷更新日期:2019-12-05 类型:月考试卷
一、单选题
-
1. 在下列方程中,一元二次方程是( )A、 B、 C、 D、2. 已知关于x的一元二次方程(a-1)x2-2x+1=0有两个不相等的实数根,则a的取值范围是( )A、a>2 B、a<2 C、a<2且a≠1 D、a<-23. 如图,等腰三角形ABC中,AB=AC,BD平分∠ABC,∠A=36°,则∠BDC的度数为( )
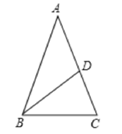 A、36° B、60° C、108° D、72°4. 某市近年来大力发展芦笋产业,某芦笋生产企业在两年内的销售额从10万元增加到70万元.设这两年的销售额的年平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、5. 在平面直角坐标系 中,以点 为圆心,4为半径的圆( )A、与 轴相交,与 轴相切 B、与 轴相离,与 轴相交 C、与 轴相切,与 轴相交 D、与 轴相切,与 轴相离6. 如图,点A,B,C,D都在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠ADC的度数为( )
A、36° B、60° C、108° D、72°4. 某市近年来大力发展芦笋产业,某芦笋生产企业在两年内的销售额从10万元增加到70万元.设这两年的销售额的年平均增长率为 ,根据题意可列方程为( )A、 B、 C、 D、5. 在平面直角坐标系 中,以点 为圆心,4为半径的圆( )A、与 轴相交,与 轴相切 B、与 轴相离,与 轴相交 C、与 轴相切,与 轴相交 D、与 轴相切,与 轴相离6. 如图,点A,B,C,D都在⊙O上,O点在∠D的内部,四边形OABC为平行四边形,则∠ADC的度数为( ) A、30° B、45° C、60° D、90°7. 设 是方程 的两个实数根,则 的值( )A、2018 B、2019 C、2017 D、20208. 如图,半径为10的⊙ 中,弦 , 所对的圆心角分别是 , ,若 , ,则弦 的长等于( )
A、30° B、45° C、60° D、90°7. 设 是方程 的两个实数根,则 的值( )A、2018 B、2019 C、2017 D、20208. 如图,半径为10的⊙ 中,弦 , 所对的圆心角分别是 , ,若 , ,则弦 的长等于( )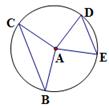 A、18 B、16 C、10 D、8
A、18 B、16 C、10 D、8二、填空题
-
9. 一元二次方程x2=2x的解为.10. 关于x的一元二次方程2x2+2x﹣m=0有实根,则m的取值范围是 .11. 如图,在 中, , ,以点 为圆心,以3 为半径作圆 ,当 时, 与圆 相切.
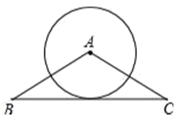 12. 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD=.
12. 如图,AB为⊙O的直径,CD为⊙O的弦,∠ACD=54°,则∠BAD=.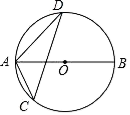 13. 一元二次方程x2-ax+6=0, 配方后为(x-3)2=3, 则a=.14. 如图,在 中, , , 的内切圆圆 与边 分别相切于点 、 、 ,则 的度数为 .
13. 一元二次方程x2-ax+6=0, 配方后为(x-3)2=3, 则a=.14. 如图,在 中, , , 的内切圆圆 与边 分别相切于点 、 、 ,则 的度数为 .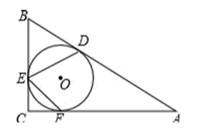 15. 当 时,代数式 比代数式 的值大2.16. 若直角三角形 的两条直角边 的长分别是5 和12 ,则此直角三角形外接圆半径为 .17. 已知方程 的两根为 , ,则 .18. 如图,以 为圆心,半径为2的圆与 轴交于 、 两点,与 轴交于 , 两点,点 为圆 上一动点, 于 ,当点 在圆 的运动过程中,线段 的长度的最小值为.
15. 当 时,代数式 比代数式 的值大2.16. 若直角三角形 的两条直角边 的长分别是5 和12 ,则此直角三角形外接圆半径为 .17. 已知方程 的两根为 , ,则 .18. 如图,以 为圆心,半径为2的圆与 轴交于 、 两点,与 轴交于 , 两点,点 为圆 上一动点, 于 ,当点 在圆 的运动过程中,线段 的长度的最小值为.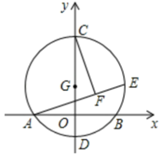
三、解答题
-
19. 解下列方程组:(1)、(2)、3x2−5x+1=020. 已知关于 x 的方程
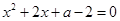 . (1)、若该方程有两个不相等的实数根,求实数
. (1)、若该方程有两个不相等的实数根,求实数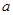 的取值范围; (2)、若该方程的一个根为1,求
的取值范围; (2)、若该方程的一个根为1,求 的值及该方程的另一根. 21. 如图,在⊙O中,点C是 的中点,弦AB与半径OC相交于点D,AB=12,CD=2.求⊙O半径的长.
的值及该方程的另一根. 21. 如图,在⊙O中,点C是 的中点,弦AB与半径OC相交于点D,AB=12,CD=2.求⊙O半径的长. 22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.若商场获得了10000元销售利润,求该玩具销售单价应定为多少元?23. 如图,已知 ,以 为直径, 为圆心的半圆交 于点 ,点 为弧 的中点,连接 交 于点 , 为 的角平分线,且 ,垂足为点 .判断直线 与 的位置关系,并说明理由;
22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.若商场获得了10000元销售利润,求该玩具销售单价应定为多少元?23. 如图,已知 ,以 为直径, 为圆心的半圆交 于点 ,点 为弧 的中点,连接 交 于点 , 为 的角平分线,且 ,垂足为点 .判断直线 与 的位置关系,并说明理由; 24. 如图,在 中, ,以斜边 上的中线 为直径作 ,分别与 、 交于点 、 .
24. 如图,在 中, ,以斜边 上的中线 为直径作 ,分别与 、 交于点 、 .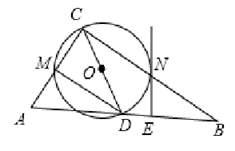 (1)、过点 作 的切线 与 相交于点 ,求证: ;(2)、连接 ,求证: .25. 如图,在⊙O中,将 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)、过点 作 的切线 与 相交于点 ,求证: ;(2)、连接 ,求证: .25. 如图,在⊙O中,将 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.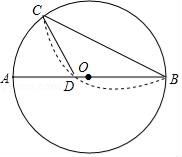 (1)、若点D恰好与点O重合,则∠ABC=°;(2)、延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.26. 对于三个数 、 、 ,用 表示这三个数的中位数,用 表示这三个数中最大数,例如: , , .
(1)、若点D恰好与点O重合,则∠ABC=°;(2)、延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.26. 对于三个数 、 、 ,用 表示这三个数的中位数,用 表示这三个数中最大数,例如: , , .解决问题:
(1)、填空:如果 ,则 的取值范围为;(2)、如果 ,求 的值.27. 如图①,已知线段 和直线 ,用直尺和圆规在 上作出所有的点 ,使得 ,如图②,小明的作图方法如下:第一步:分别以点 , 为圆心, 长为半径作弧,两弧在 上方交于点 ;
第二步:连接 , ;
第三步:以 为圆心, 长为半径作 ,交 于 , ;
所以图中 , 即为所求的点.
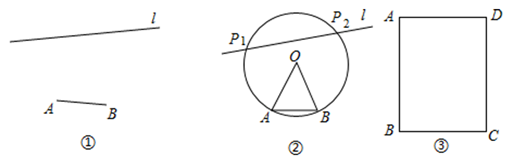 (1)、在图②中,连接 , ,说明 ;(2)、(方法迁移)如图③,用直尺和圆规在矩形 内作出所有的点 ,使得 (不写作法,保留作图痕迹).(3)、(深入探究)已知矩形 , , , 为 边上的点,若满足 的点 恰有两个,求 的取值范围.(4)、已知矩形 , , , 为矩形 内一点,且 ,若点 绕点 逆时针旋转 到点 ,求 的最小值.
(1)、在图②中,连接 , ,说明 ;(2)、(方法迁移)如图③,用直尺和圆规在矩形 内作出所有的点 ,使得 (不写作法,保留作图痕迹).(3)、(深入探究)已知矩形 , , , 为 边上的点,若满足 的点 恰有两个,求 的取值范围.(4)、已知矩形 , , , 为矩形 内一点,且 ,若点 绕点 逆时针旋转 到点 ,求 的最小值.