江苏省淮安市清江浦区2020届九年级上学期数学10月月考试卷
试卷更新日期:2019-12-05 类型:月考试卷
一、单选题
-
1. 下列方程是一元二次方程的是( )A、x+2y=1 B、 C、 D、2. 如图,△ABC中,∠A=78°,AB=4,BC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是( )
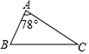 A、
A、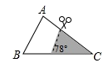 B、
B、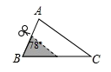 C、
C、 D、
D、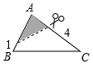 3. 关于x的一元二次方程 的两根为 , 那么下列结论一定成立的是( )A、 B、 C、 D、4. 如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2 , 则修建的路宽应为( )
3. 关于x的一元二次方程 的两根为 , 那么下列结论一定成立的是( )A、 B、 C、 D、4. 如图,在宽为20米、长为30米的矩形地面上修建两条同样宽的道路,余下部分作为耕地.若耕地面积需要551米2 , 则修建的路宽应为( )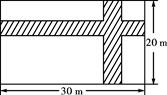 A、1米 B、1.5米 C、2米 D、2.5米5. 如图,DE∥BC, ,那么△ADE与△ABC的相似比为 ( )
A、1米 B、1.5米 C、2米 D、2.5米5. 如图,DE∥BC, ,那么△ADE与△ABC的相似比为 ( )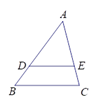 A、 B、 C、 D、26. 如图,梯形ABCD中,AD//BC,对角线AC、BD相交于点O ,若 ,则 等于( )
A、 B、 C、 D、26. 如图,梯形ABCD中,AD//BC,对角线AC、BD相交于点O ,若 ,则 等于( )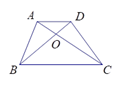 A、1:6 B、1:3 C、1:4 D、1:5
A、1:6 B、1:3 C、1:4 D、1:5二、填空题
-
7. 方程x2=3x的解为 .8. 若 ,则 =9. 关于x的方程 有解,则b的取值范围是10. 如图,已知 ∽ , ,则 的长为.
 11. 线段2cm、8cm的比例中项为cm.
11. 线段2cm、8cm的比例中项为cm.
12. 若a︰b︰c=2︰3︰4,且2a+3b-c=18,则a+2b+c=13. 一个三角形的两边长分别为4cm和7cm,第三边长是一元二次方程x2﹣10x+21=0的实数根,则三角形的周长是cm.14. 如图,在△ABC中,D是△ABC的重心, ,则△AEC的面积是 15. 如图,在平行四边形ABCD,点E在BC上,AE、BD相交于点F,若BE=3,EC=5,BF=2.7,则FD= .
15. 如图,在平行四边形ABCD,点E在BC上,AE、BD相交于点F,若BE=3,EC=5,BF=2.7,则FD= .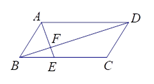 16. 如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为 , , ,…, 的n 个正方形依次放入△ABC中,则第n个正方形的边长 (用含n的式子表示).
16. 如图所示,在Rt△ABC中,∠C=90°,BC=1,AC=4,把边长分别为 , , ,…, 的n 个正方形依次放入△ABC中,则第n个正方形的边长 (用含n的式子表示).
三、解答题
-
17. 解方程(1)、(2)、(3)、(4)、18. 如图,在11×11的正方形网格中,△TAB的顶点分别为T(1,1),A(2,3),B(4,2).
 (1)、以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 , 点B′的坐标为(2)、在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .19. 已知:关于x的方程(1)、求证:不论m取何值时,方程总有两个不相等的实数根(2)、若方程的一个根为1,求m的值及方程的另一根20. 如图, ∽ .
(1)、以点T(1,1)为位似中心,按比例尺(TA′:TA)3:1,在位似中心的同侧将△TAB放大为△TA′B′,放大后点A,B的对应点分别为A′,B′,画出△TA′B′,并写出点A′,B′的坐标;点A′的坐标为 , 点B′的坐标为(2)、在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标为 .19. 已知:关于x的方程(1)、求证:不论m取何值时,方程总有两个不相等的实数根(2)、若方程的一个根为1,求m的值及方程的另一根20. 如图, ∽ . (1)、求 的大小;(2)、求 的长.21. 如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2.如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.
(1)、求 的大小;(2)、求 的长.21. 如图①,窗帘的褶皱是指按照窗户的实际宽度将窗帘布料以一定比例加宽的做法,褶皱之后的窗帘更能彰显其飘逸、灵动的效果.其中,窗宽度的1.5倍为平褶皱,窗宽度的2倍为波浪褶皱.如图②,小莉房间的窗户呈长方形,窗户的宽度(AD)比高度(AB)的少0.5m,某种窗帘的价格为120元/m2.如果以波浪褶皱的方式制作该种窗帘比以平褶皱的方式费用多180元,求小莉房间窗户的宽度与高度.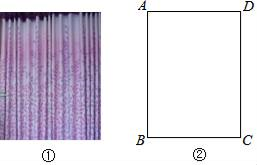 22. 如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若 ,AC=14,
22. 如图,已知AD∥BE∥CF,它们以此交直线l1、l2于点A、B、C和D、E、F.若 ,AC=14,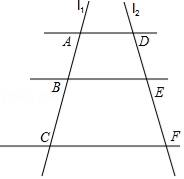 (1)、求AB的长.(2)、如果AD=7,CF=14,求BE的长.23. 爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.
(1)、求AB的长.(2)、如果AD=7,CF=14,求BE的长.23. 爱动脑筋的小明在学过用配方法解一元二次方程后,他发现二次三项式也可以配方,从而解决一些问题.例如: ;因此 有最小值是1,只有当 时,才能得到这个式子的最小值1.
同样 ,因此 有最大值是8,只有当 时,才能得到这个式子的最大值8.
 (1)、当x=时,代数式﹣2(x﹣3)2+5有最大值为 .(2)、当x=时,代数式2x2+4x+3有最小值为 .(3)、矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?24. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的 速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.
(1)、当x=时,代数式﹣2(x﹣3)2+5有最大值为 .(2)、当x=时,代数式2x2+4x+3有最小值为 .(3)、矩形自行车场地ABCD一边靠墙(墙长10m),在AB和BC边各开一个1米宽的小门(不用木板),现有能围成14m长的木板,当AD长为多少时,自行车场地的面积最大?最大面积是多少?24. 如图1,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从A出发沿AC向C点以1厘米/秒的速度匀速移动;点Q从C出发沿CB向B点以2厘米/秒的 速度匀速移动.点P、Q分别从起点同时出发,移动到某一位置时所需时间为t秒.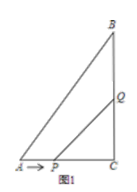
(1)、当t=时,PQ∥AB(2)、当t为何值时,△PCQ的面积等于5cm2?(3)、在P、Q运动过程中,在某一时刻,若将△PQC翻折,得到△EPQ,如图2,PE与AB能否垂直?若能,求出相应的t值;若不能,请说明理由.能垂直,理由如下:
延长QE交AC于点D,

∵将△PQC翻折,得到△EPQ,
∴△QCP≌△QEP,
∴∠C=∠QEP=90°,
若PE⊥AB,则QD∥AB,
∴△CQD∽△CBA,
∴ ,
∴ ,
∴QD=2.5t,
∵QC=QE=2t
∴DE=0.5t
∵∠A=∠EDP,∠C=∠DEP=90°,
∴△ABC∽△DPE,
∴
∴ ,
解得: ,
综上可知:当t= 时,PE⊥AB
 25. 如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB•AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.
25. 如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=AB•AD,我们称该四边形为“可分四边形”,∠DAB称为“可分角”.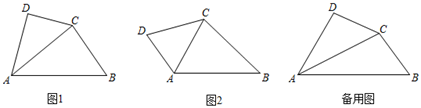 (1)、如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.(2)、如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=°(3)、现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长.
(1)、如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,求证:△DAC∽△CAB.(2)、如图2,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则∠DAB=°(3)、现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,BC=2,∠D=90°,求AD的长.