江苏省东台市联谊校2020届九年级上学期数学10月月考试卷
试卷更新日期:2019-12-05 类型:月考试卷
一、单选题
-
1. 已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是 ( )A、点P在⊙O上 B、点P在⊙O内 C、点P在⊙O外 D、无法判断2. 用配方法解方程 ,下列配方正确的是( )A、 B、 C、 D、3. 如图,在⊙O中, ,若∠B=75°,则∠C的度数为( )
 A、15° B、30° C、75° D、.60°4. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( )
A、15° B、30° C、75° D、.60°4. 如图,点A,B,C在⊙O上,∠AOB=72°,则∠ACB等于( ) A、28° B、54° C、18° D、36°5. 下列说法正确的是( )A、相等的圆心角所对的弧相等 B、90°的角所对的弦是直径 C、等弧所对的弦相等 D、圆的切线垂直于半径6. 关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是( )A、 B、 C、 D、 且7. 如图,P为⊙O内一点,过点P的最长的弦长为4cm,最短的弦长为2cm,则OP的长为( )A、1cm B、2cm C、 cm D、 cm8. 如图,半径为10的⊙ 中,弦 , 所对的圆心角分别是 , ,若 , ,则弦 的长等于( )
A、28° B、54° C、18° D、36°5. 下列说法正确的是( )A、相等的圆心角所对的弧相等 B、90°的角所对的弦是直径 C、等弧所对的弦相等 D、圆的切线垂直于半径6. 关于x的一元二次方程kx2+2x-1=0有两个不相等的实数根,则k的取值范围是( )A、 B、 C、 D、 且7. 如图,P为⊙O内一点,过点P的最长的弦长为4cm,最短的弦长为2cm,则OP的长为( )A、1cm B、2cm C、 cm D、 cm8. 如图,半径为10的⊙ 中,弦 , 所对的圆心角分别是 , ,若 , ,则弦 的长等于( )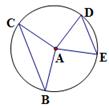 A、18 B、16 C、10 D、8
A、18 B、16 C、10 D、8二、填空题
-
9. 写出解为 的一个一元二次方程:.10. 若菱形的两条对角线长分别是方程 的两实根,则菱形的面积为.11. 如图,正六边形ABCDEF内接于半径为4的圆,则B、E两点间的距离为.
 12. 某小区准备在每两幢楼房之间开辟一块面积为300平方米的矩形绿地,且长比宽多7米,设长方形绿地的宽为 米,则可列方程为.13.
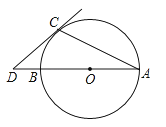
12. 某小区准备在每两幢楼房之间开辟一块面积为300平方米的矩形绿地,且长比宽多7米,设长方形绿地的宽为 米,则可列方程为.13.如图,AB是⊙O的直径,点D在AB的延长线上,DC切⊙O于点C,若∠A=25°,则∠D等于 .
 14. 如图,在 中,AB=AC,BC=4,以 为直径作半圆 ,交 于点 ,则 的长是.
14. 如图,在 中,AB=AC,BC=4,以 为直径作半圆 ,交 于点 ,则 的长是.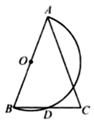 15. 已知x=m是方程x2-2x-3=0的根,则代数式2m2-4m-3的值为.16. 如图,在平面直角坐标系中,直线l的函数表达式为 ,点 的坐标为(1,0),以 为圆心, 为半径画圆,交直线 于点 ,交 轴正半轴于点 ,以 为圆心, 为半径的画圆,交直线 于点 ,交 轴的正半轴于点 ,以 为圆心, 为半径画圆,交直线 与点 ,交 轴的正半轴于点 ,… 按此做法进行下去,其中弧 的长为.
15. 已知x=m是方程x2-2x-3=0的根,则代数式2m2-4m-3的值为.16. 如图,在平面直角坐标系中,直线l的函数表达式为 ,点 的坐标为(1,0),以 为圆心, 为半径画圆,交直线 于点 ,交 轴正半轴于点 ,以 为圆心, 为半径的画圆,交直线 于点 ,交 轴的正半轴于点 ,以 为圆心, 为半径画圆,交直线 与点 ,交 轴的正半轴于点 ,… 按此做法进行下去,其中弧 的长为.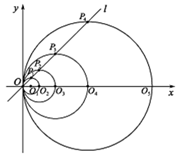
三、解答题
-
17. 解方程:(1)、(2)、18. 某工厂今年3月份的产值为100万元,由于受国际金融风暴的影响,5月份的产值下降到81万元,求平均每月产值下降的百分率.
19. 已知:如图,OA,OB为☉O的半径,C,D分别为OA,OB的中点,求证:AD=BC.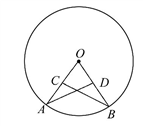 20. 小林准备进行如下操作试验:把一根长为 的铁丝剪成两段,并把每一段各围成一个正方形.(1)、要使这两个正方形的面积之和等于 ,小林该怎么剪?(2)、小峰对小林说:“这两个正方形的面积之和不可能等于 .”他的说法对吗?请说明理由.21. 如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.
20. 小林准备进行如下操作试验:把一根长为 的铁丝剪成两段,并把每一段各围成一个正方形.(1)、要使这两个正方形的面积之和等于 ,小林该怎么剪?(2)、小峰对小林说:“这两个正方形的面积之和不可能等于 .”他的说法对吗?请说明理由.21. 如图,AB为⊙O的直径,点C,D在⊙O上,且BC=6 cm,AC=8 cm,∠ABD=45°.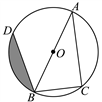 (1)、求BD的长;(2)、求图中阴影部分的面积.22. 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)、求BD的长;(2)、求图中阴影部分的面积.22. 如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.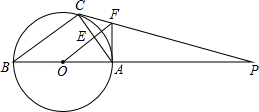 (1)、判断AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为4,AF=3,求AC的长.23. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.
(1)、判断AF与⊙O的位置关系并说明理由;(2)、若⊙O的半径为4,AF=3,求AC的长.23. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E.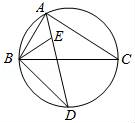 (1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.24. 已知⊙ 中, 为直径, 、 分别切⊙ 于点 、 .
(1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.24. 已知⊙ 中, 为直径, 、 分别切⊙ 于点 、 .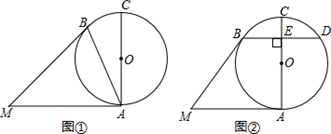 (1)、如图①,若 ,求 的大小;(2)、如图②,过点 作 ∥ ,交 于点 ,交⊙ 于点 ,若 ,求 的大小.25. 实践操作
(1)、如图①,若 ,求 的大小;(2)、如图②,过点 作 ∥ ,交 于点 ,交⊙ 于点 ,若 ,求 的大小.25. 实践操作如图, 是直角三角形, ,利用直尺和圆规按下列要求作图,并在图中表明相应的字母.(保留作图痕迹,不写作法)
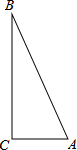 (1)、①作 的平分线,交 于点 ;②以 为圆心, 为半径作圆.
(1)、①作 的平分线,交 于点 ;②以 为圆心, 为半径作圆.综合运用在你所作的图中,
(2)、 与⊙ 的位置关系是;(直接写出答案)(3)、若 , ,求⊙ 的半径.(4)、在(3)的条件下,求以 为轴把△ABC旋转一周得到的圆锥的侧面积.26. 问题背景:如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= CD,从而得出结论:AC+BC= CD.
简单应用:
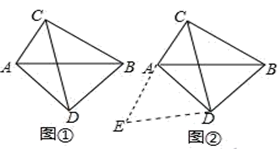
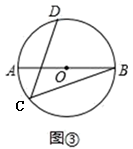
 (1)、在图①中,若AC=2,BC=4,则CD=.(2)、如图③,AB是⊙O的直径,点C、D在⊙上,弧AD=弧BD,若AB=13,BC=12,求CD的长.拓展规律:(3)、如图4,△ABC中,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是.
(1)、在图①中,若AC=2,BC=4,则CD=.(2)、如图③,AB是⊙O的直径,点C、D在⊙上,弧AD=弧BD,若AB=13,BC=12,求CD的长.拓展规律:(3)、如图4,△ABC中,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= AC,CE=CA,且点E在直线AC的左侧时,点Q为AE的中点,则线段PQ与AC的数量关系是.