湖北省武汉市硚口区2020届九年级上学期数学10月月考试卷

试卷更新日期：2019-12-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 方程 $2 x^{2} - 6 x = 9$ 的二次项系数是2，则一次项系数，常数项分别为（）

A、6，-9 B、-6，9 C、-6，-9 D、6，9

查看试题解析
2. 已知 $x = 2$ 是关于 $x$ 的方程 $x^{2} - 2 a = 0$ 的一个解，则 $a$ 的值是（）

A、2 B、-2 C、1 D、-1

查看试题解析
3. 用配方法解方程 $x^{2} - 10 x + 9 = 0$ ，配方后正确的是（）

A、 ${(x - 5)}^{2} = 16$ B、 ${(x + 5)}^{2} = 1$ C、 ${(x - 10)}^{2} = 91$ D、 ${(x + 10)}^{2} = 109$

查看试题解析
4. 某树主干长出若干数目的支干，每个支干又长出同样数目小分支，主干、支干和小分支总数共31.若设主干长出 $x$ 个支干，则所列方程正确的是（）

A、 ${(1 + x)}^{2} = 31$ B、 $1 + x + x^{2} = 31$ C、 $(1 + x) x = 31$ D、 $1 + x + 2 x = 31$

查看试题解析
5. 某校去年对实验器材的投资为2万元，预计今明两年的投资总额为8万元，若设该校今明两年在实验器材投资上的年平均增长率是x，则所列方程正确的是（）

A、 $2 {(1 + x)}^{2} = 8$ B、 $2 (1 + x) + 2 {(1 + x)}^{2} = 8$ C、 $2 (1 + 2 x) = 8$ D、 $2 (1 + x^{2}) = 8$

查看试题解析
6. 已知点 $A (- 3, y_{1})$ ， $B (- 2, y_{2})$ 在函数 $y = - x^{2} - 2 x + b$ 的图象上，则下列说法正确的是（）

A、 $y_{1} + y_{2} > 0$ B、 $y_{1} > y_{2}$ C、 $y_{1} = y_{2}$ D、 $y_{1} < y_{2}$

查看试题解析
7. 如图是一个长 $18 c m$ ，宽 $15 c m$ 的矩形图案，其中有两条宽度相等，互相垂直的彩条，彩条面积是图案面积的三分之一，设彩条的宽度为 $x c m$ ，则所列方程正确的是（）

A、 $18 x + 15 x - 2 x^{2} = \frac{1}{3} \times 15 \times 18$ B、 $18 x + 15 x = \frac{1}{3} \times 15 \times 18$ C、 $(18 - x) (15 - x) = \frac{2}{3} \times 15 \times 18$ D、 $18 x + 15 x + x^{2} = \frac{1}{3} \times 15 \times 18$

查看试题解析
8. 二次函数 $y = x^{2} - a x + b$ 的图象如图所示，对称轴为直线 $x = 2$ ，下列结论不正确的是（）

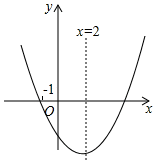A、 $a = 4$ B、当 $b = - 4$ 时，顶点的坐标为 $(2 ， - 8)$ C、当 $x = - 1$ 时， $b > - 5$ D、当 $x > 3$ 时，y随x的增大而增大

查看试题解析
9. 一位篮球运动员在距离篮圈中心水平距离4m处起跳投篮，球沿一条抛物线运动，当球运动的水平距离为2.5m时，达到最大高度3.5m，然后准确落入篮框内．已知篮圈中心距离地面高度为3.05m，在如图所示的平面直角坐标系中，下列说法正确的是（）

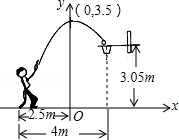A、此抛物线的解析式是y=﹣ $\frac{1}{5}$ x²+3.5 B、篮圈中心的坐标是（4，3.05） C、此抛物线的顶点坐标是（3.5，0） D、篮球出手时离地面的高度是2m

查看试题解析
10. 在平面直角坐标系中，已知 $a \neq b$ ，函数 $y = (x + a) (x + b)$ 的图象与 $x$ 轴有 $m$ 个交点，函数 $y = (a x + 1) (b x + 1)$ 的图象与 $x$ 轴有 $n$ 个交点，则 $m$ 与 $n$ 的数量关系是（）

A、 $m = n$ B、 $m = n - 1$ 或 $m = n + 2$ C、 $m = n$ 或 $m = n + 1$ D、 $m = n$ 或 $m = n - 1$

查看试题解析

二、填空题

11. 一元二次方程 $x^{2} - 9 = 0$ 的解是．

查看试题解析
12. 篮球联赛实行单循环赛制，即每两个球队之间进行一场比赛，一共打45场比赛.设有 $x$ 个球队参赛，根据题意，所列方程为.

查看试题解析
13. 某商品的进价为每件40元，现在的售价为每件60元，每星期可卖出300件.市场调查反映：如调整价格，每降价1元，每星期可多卖出20件.则每周售出商品的利润 $y$ （单位：元）与每件降价 $x$ （单位：元）之间的函数关系式为.（化成一般形式）

查看试题解析
14. 如图，在 $▱ A B C D$ 中， $E$ 、 $F$ 是对角线 $A C$ 上两点， $A E = E F = C D$ ， $∠ A D F = 90^{\circ}$ ， $∠ B C D = 66^{\circ}$ ，则 $∠ A D E$ 的大小为.

查看试题解析
15. 从地面竖直向上抛出一小球，小球的高度 $h$ （米）与小球的运动时间 $t$ （秒）之间的关系式是 $h = 30 t - 5 t^{2}$ ，则小球抛出5秒共运动的路径是米.

查看试题解析
16. 点 $E$ 是 $Δ A B C$ 边上的点，点 $F$ 是边 $B C$ 的中点， $E F$ 平分 $Δ A B C$ 的面积，若 $A B = 2$ ， $∠ B A C = 120^{\circ}$ ， $A C = 4$ ，则 $E F =$ .

查看试题解析

三、解答题

17. 解方程：

(1)、 $x^{2} - 2 x - 1 = 0$

(2)、 $4 x^{2} - 6 x = 0$

(3)、 $a x^{2} + (a^{2} - 1) x - a = 0$ （ $a$ 是常数且 $a \neq 0$ ）

查看试题解析
18. 已知抛物线 $y = a x^{2}$ 经过点A(－2，－8).

(1)、求a的值，

(2)、若点P(m，－6)在此抛物线上，求点P的坐标.

查看试题解析
19. 已知函数 $y = - \frac{1}{2} {(x + 1)}^{2} - 2$ .

(1)、指出函数图象的开口方向是，对称轴是，顶点坐标为；

(2)、当x时，y随x的增大而减小；

(3)、怎样移动抛物线 $y = - \frac{1}{2} x^{2}$ 就可以得到抛物线 $y = - \frac{1}{2} {(x + 1)}^{2} - 2$ .

查看试题解析
20. 已知关于 $x$ 的一元二次方程 $x^{2} + (4 m + 1) x + 2 m - 1 = 0$ ，

(1)、求证：不论 $m$ 为任何实数，方程有两个不相等的实数根；

(2)、设方程的两根分别为 $x_{1}$ ， $x_{2}$ ，且满足 $\frac{1}{x_{1}} + \frac{1}{x_{2}} = - \frac{1}{2}$ ，求 $m$ 的值.

查看试题解析
21. 如图，一农户要建一个矩形猪舍，猪舍的一边利用长为12m的住房墙，另外三边用25m长的建筑材料围成，为方便进出，在垂直于住房墙的一边留一个1m宽的门，所围矩形猪舍的长、宽分别为多少时，猪舍面积为80m²？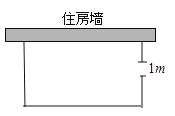

查看试题解析

22. 某商店销售一种商品，童威经市场调查发现：该商品的周销售量

y

（件）是售价

x

（元/件）的一次函数，其售价、周销售量、周销售利润

w

（元）的三组对应值如下表：

售价 $x$ （元/件）	50	60	80
周销售量 $y$ （件）	100	80	40
周销售利润 $w$ （元）	1000	1600	1600

注：周销售利润＝周销售量×（售价－进价）

(1)、①求

y

关于

x

的函数解析式（不要求写出自变量的取值范围）

②该商品进价是元/件；当售价是元/件时，周销售利润最大，最大利润是元

(2)、由于某种原因，该商品进价提高了

m

元/件

(m > 0)

，物价部门规定该商品售价不得超过65元/件，该商店在今后的销售中，周销售量与售价仍然满足（1）中的函数关系.若周销售最大利润是1400元，求

m

的值

查看试题解析

23. 在正方形 $A B C D$ 中， $A B = 4$ ，点 $H$ ， $E$ ， $F$ 分别在边 $A B$ ， $B C$ ， $C D$ 上，且 $A E$ 垂直 $H F$ .

(1)、如图1，求证： $A E = H F$ ；

(2)、如图2，平移线段 $H F$ 至线段 $B G$ ， $B G$ 交 $A E$ 于点 $O$ ，图中阴影部分的面积与正方形的面积之比为 $3 ： 4$ ，求 $Δ A B O$ 的周长；

(3)、如图3，若 $B H = D F$ ，将线段 $H F$ 绕点 $F$ 顺时针旋转 $90^{\circ}$ 至线段 $M F$ ，连接 $A M$ ，则线段 $A M$ 的最小值为.

查看试题解析
24. 已知抛物线 $C$ 的顶点坐标为 $A (0 ， - 2)$ ，经过点 $B (4 ， 6)$ .

(1)、求抛物线 $C$ 的解析式；

(2)、如图1，直线 $y = k x - 4 (k > 0)$ 交抛物线 $C$ 于 $M$ ， $N$ 两点，若 $S_{Δ A M N} = 1$ ，求 $k$ 的值；

(3)、如图2，将抛物线 $C$ 向下平移 $m (m > 0)$ 个单位长度得到抛物线 $C_{1}$ ，抛物线 $C_{1}$ 的顶点为 $P$ ，交 $x$ 轴的负半轴于点 $E$ ，点 $F (a ， 2 a - 2) (a > 2)$ 在抛物线 $C_{1}$ 上.
①求点 $E$ 的坐标（用含 $a$ 的式子表示）；

②若 $∠ F E O = 2 ∠ E F P$ ，求 $a$ ， $m$ 的值.

查看试题解析