湖北省黄石市部分区2020届九年级上学期数学10月月考试卷
试卷更新日期:2019-12-05 类型:月考试卷
一、单选题
-
1. 方程 的二次项系数、一次项系数、常数项分别为( )A、6,2,9 B、2,-6,9 C、-2,-6,9 D、2,-6,-92. 方程 的解是( )A、x=2 B、x=3 C、x=-1,或x=2 D、x=-1,或x=33. 由二次函数 ,可知( )A、其图象的开口向下 B、其图象的对称轴为直线 C、其最小值为1 D、当x<3时,y随x的增大而增大4. 使分式 的值等于零的x的值是( )A、1或6 B、2或3 C、3 D、25. 已知四点A(0,-2),B(1,0),C(2,0),D(0,4)若一个二次函数的图象经过这四点中的三点,则这个二次函数图象的对称轴为( )A、x= B、x=-3 C、x=3 D、x=6. 如图,抛物线y=ax2+bx+c的部分图象与x轴交于点(3,0)对称轴为直线x=1,对于整个抛物线来说,当y≤0时,x的取值范围是( )
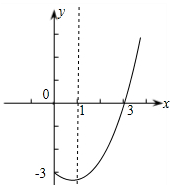 A、0<x≤3 B、-2 x≤3 C、-1≤x≤3 D、x≤-1或x≥37. 某医院内科病房有护士x人,每2人一班,轮流值班,每8小时換班一次,某两人同值班后,到下次两人再同班,最长需要的天数是70天,则x=( )A、15 B、18 C、21 D、358. 如表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )
A、0<x≤3 B、-2 x≤3 C、-1≤x≤3 D、x≤-1或x≥37. 某医院内科病房有护士x人,每2人一班,轮流值班,每8小时換班一次,某两人同值班后,到下次两人再同班,最长需要的天数是70天,则x=( )A、15 B、18 C、21 D、358. 如表是满足二次函数 的五组数据, 是方程 的一个解,则下列选项中正确的是( )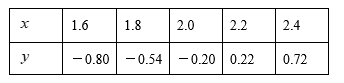 A、 B、 C、 D、9. 已知函数 ,并且 , 是方程 的两个根,则实数 , , , 的大小关系可能是( )A、 B、 C、 D、10. 二次函数 图象如图,下列结论:① ;② ;③当 时, ;④ ;⑤若 ,且 ,则 .其中正确的有( )
A、 B、 C、 D、9. 已知函数 ,并且 , 是方程 的两个根,则实数 , , , 的大小关系可能是( )A、 B、 C、 D、10. 二次函数 图象如图,下列结论:① ;② ;③当 时, ;④ ;⑤若 ,且 ,则 .其中正确的有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
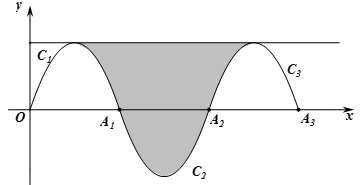
11. 已知方程 的两根是 、 ,则 .12. 某工厂生产一种产品,第一季度共生产了364个.其中1月份生产了100个,若2、3月份的平均月增长率为x,则可列方程为13. 二次函数y=x2+6x+5图象的顶点坐标为 .14. 已知一元二次方程2x2+bx+c=0的两根为x1=-2,x2=3.那么多项式2x2+bx+c可因式分解为15. 已知 , 是抛物线 上的两点,且 ,若 ,则 (填“ ”、“ ”或“ ”)16. 如图,一段抛物线: ,记为 ,它与 轴交于两点 , :将 绕 旋转 得到 ,交 轴于 :将 绕 旋转 得到 ,交 轴于 .过抛物线 , 顶点的直线与 , , 围成的如图中的阴影部分,那么该面积为.
三、解答题
-
17. 用适当的方法解下列一元二次方程(1)、(2x-1)2=25(2)、3x2-6x-1=0(3)、x2-4x-396=0(4)、(2-3x)+(3x-2)2=018. 已知:a是方程x2+4x-1=0的根求代数式 ÷(a+3- )的值19. 已知关于x的方程x2﹣2x+m=0有两个不相等的实数根x1、x2
(1)、求实数m的取值范围;(2)、若x1﹣x2=2,求实数m的值.
20. 有一人患了流感,经过两轮传染后共有64人患了流感.(1)、求每轮传染中平均一个人传染了几个人?(2)、如果不及时控制,第三轮将又有多少人被传染?21. 如图: 斜边 的中垂线交 边于点 ,若 , ,求 的长.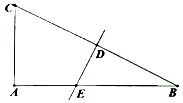 22. 已知抛物线y= x2-mx+c与x轴交于点A(x1 , 0)B(x2 , 0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值
22. 已知抛物线y= x2-mx+c与x轴交于点A(x1 , 0)B(x2 , 0),与y轴交于点C(0,c).若△ABC为直角三角形,求c的值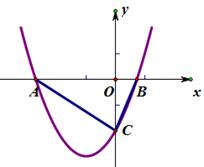 23. 经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
23. 经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元.
(1)、求出y与x的函数关系式(2)、问销售该商品第几天时,当天销售利润最大?最大利润是多少?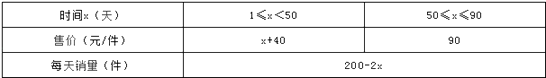 .24. 如图, 是边长为 的等边三角形,动点 、 同时从 、 两点出发,分别沿 、 方向匀速移动,它们的速度都是 ,当点 到达点 时, 、 两点停止运动,设点 的运动时间 .
.24. 如图, 是边长为 的等边三角形,动点 、 同时从 、 两点出发,分别沿 、 方向匀速移动,它们的速度都是 ,当点 到达点 时, 、 两点停止运动,设点 的运动时间 .解答下列各问题:
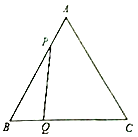 (1)、求 的面积(2)、当 为何值时, 是直角三角形?(3)、设四边形 的面积为 ,求 与 的关系式;是否存在某一时刻 ,使四边形 的面积是 面积的三分之二?如果存在,求出 的值;不存在请说明理由25. 已知直线l:y=kx+4与抛物线y= x2交于点A(x1 , y1),B(x2 , y2).(1)、求: ; 的值.(2)、过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.(3)、证明: + 为定值,并求出该值.
(1)、求 的面积(2)、当 为何值时, 是直角三角形?(3)、设四边形 的面积为 ,求 与 的关系式;是否存在某一时刻 ,使四边形 的面积是 面积的三分之二?如果存在,求出 的值;不存在请说明理由25. 已知直线l:y=kx+4与抛物线y= x2交于点A(x1 , y1),B(x2 , y2).(1)、求: ; 的值.(2)、过点(0,-4)作直线PQ∥x轴,且过点A、B分别作AM⊥PQ于点M,BN⊥PQ于点N,设直线l:y=kx+4交y轴于点F.求证:AF=AM=4+y1.(3)、证明: + 为定值,并求出该值.