河南省郑州市中原区2020届九年级上学期数学10月月考试卷

试卷更新日期：2019-12-05 类型：月考试卷

进入出卷网下载

一、单选题

1. 下列条件中，能判断四边形是菱形的是（）

A、对角线互相垂直且相等的四边形 B、对角线互相垂直的四边形 C、对角线相等的平行四边形 D、对角线互相平分且垂直的四边形

查看试题解析
2. 把一元二次方程x（x+1）＝3x+2化为一般形式，正确的是（）

A、x²+4x+3＝0 B、x²﹣2x+2＝0 C、x²﹣3x﹣1＝0 D、x²﹣2x﹣2＝0

查看试题解析
3. 若a、b是关于x的一元二次方程x²﹣6x+n+1=0的两根，且等腰三角形三边长分别为a、b、4，则n的值为（）

A、8 B、7 C、8或7 D、9或8

查看试题解析
4. 一个盒子中装有标号为1，2，3，4，5的五个小球，这些球除标号外都相同，从中随机摸出两个小球，则摸出的小球标号之和大于5的概率为（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
5. 为执行“均衡教育“政策，某区2017年投入教育经费2500万元，预计到2019年底三年累计投入1.2亿元，若每年投入教育经费的年平均增长百分率为x，则下列方程正确的是（）

A、2500(1+2x)=12000 B、2500+2500(1+x)+2500(1+2x)=12000 C、2500(1+x)²=1200 D、2500+2500(1+x)+2500(1+x)²=12000

查看试题解析
6. 下列数中，能与6，9，10组成比例的数是（）

A、1 B、74 C、5.4 D、1.5

查看试题解析
7. 如图，菱形ABCD的两条对角线AC，BD相交于点O，E是AB的中点，若AC＝6，菱形ABCD的面积为24，则OE长为（）

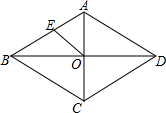A、2.5 B、3.5 C、3 D、4

查看试题解析
8. 如图，矩形ABCD，点E. F分别在AD、BC上且AE=DE，BC=3BF，连接EF，将矩形ABCD沿EF折叠，点A恰好落在BC边上的点G处，若AB= $\sqrt{5}$ ，则CG为（）

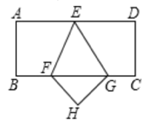A、3. B、1. C、2. D、 $\sqrt{2}$ .

查看试题解析

二、填空题

9. 已知 $\frac{a}{b} = \frac{2}{3}$ ，则 $\frac{a + b}{3 a - b} =$ .

查看试题解析
10. 如图所示，长为8cm，宽为6cm的矩形中，截去一个矩形（图中阴影部分），如果剩下矩形与原矩形相似，那么剩下矩形的面积是

查看试题解析
11. 若(m-1) $x^{m (m + 2) - 1}$ +2mx-1=0是关于x的一元二次方程，则m的值是.

查看试题解析
12. 在一个不透明的袋子中装有20个蓝色小球、若干个红色小球和10个黄色小球，这些球除颜色不同外其余均相同，小李通过多次摸取小球试验后发现，摸取到红色小球的频率稳定在0.4左右，若小明在袋子中随机摸取一个小球，则摸到黄色小球的概率为

查看试题解析
13. 如图，在正方形ABCD中，AD=1，将△ABD绕点B顺时针旋转45°得到△A′BD′，此时A′D′与CD交于点E，则DE的长度为.

查看试题解析
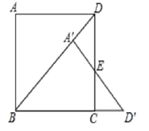14. 如图，菱形ABCD的边长为4，∠B＝120°.点P是对角线AC上一点（不与端点A重合），则线段 $\frac{1}{2}$ AP+PD的最小值为.

查看试题解析
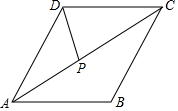15. 矩形纸片ABCD，AB=9，BC=6，在矩形边上有一点P，且DP=3．将矩形纸片折叠，使点B与点P重合，折痕所在直线交矩形两边于点E，F，则EF长为．

查看试题解析

三、解答题

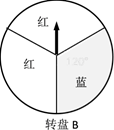
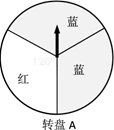
16. 用适当的方法解下列方程：

(1)、 $x^{2} - 4 x = 12$

(2)、 $3 x (x - 2) = 2 x - 4$

查看试题解析
17. 某商场在促销活动中规定，顾客每消费100元就能获得一次抽奖机会.为了活跃气氛，设计了两个抽奖方案：
方案一：转动转盘A一次，转出红色可领取一份奖品；

方案二：转动转盘B两次，两次都转出红色可领取一份奖品.（两个转盘都被平均分成3份）如果你获得一次抽奖机会，你会选择哪个方案？请用相关的数学知识说明理由.

查看试题解析
18. 如图，四边形ABCD中，对角线AC、BD相交于点O，AO=CO，BO=DO，且∠ABC+∠ADC=180°.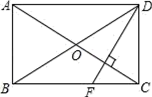

(1)、求证：四边形ABCD是矩形.

(2)、若∠ADF：∠FDC=3：2，DF⊥AC，求∠BDF的度数.

查看试题解析
19. 在一元二次方程中，有著名的韦达定理：对于一元二次方程ax²+bx+c=0(a≠0)，如果方程有两个实数根x₁ ， x₂ ，那么x₁+x₂= $- \frac{b}{a}$ ，x₁+x₂= $\frac{c}{a}$ (说明：定理成立的条件△≥0).比如方程2x²-3x-1=0中，△=17，所以该方程有两个不等的实数解.记方程的两根为x₁ ， x₂ ，那么x₁+x₂= $\frac{3}{2}$ ，x₁+x₂= $- \frac{1}{2}$ .请阅读材料回答问题：

(1)、已知方程x²-3x-2=0的两根为x₁、x₂ ，求下列各式的值：
①x₁²+x₂²；② $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ；

(2)、已知x₁ ， x₂是一元二次方程4kx²-4kx+k+1=0的两个实数根.
①是否存在实数k，使(2x₁-x₂)(x₁-2x₂)= $- \frac{3}{2}$ 成立？若存在，求出k的值；若不存在，请说明理由；

②求使 $\frac{x_{2}}{x_{1}} + \frac{x_{1}}{x_{2}}$ -2的值为整数的实数k的整数值.

查看试题解析
20. 如图1，△ABC为等腰三角形，AB=AC=a，P点是底边BC上的一个动点，PD∥AC，PE∥AB.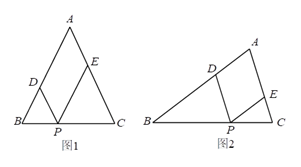

(1)、用a表示四边形ADPE的周长为；

(2)、点P运动到什么位置时，四边形ADPE是菱形，请说明理由；

(3)、如果△ABC不是等腰三角形(图2)，其他条件不变，点P运动到什么位置时，四边形ADPE是菱形(不必说明理由).

查看试题解析
21. 随着生活水平的不断提高，越来越多的人选择到电影院观看电影，体验视觉盛宴，并且更多的人通过网上平台购票，既快捷又能享受更多优惠.某电影城2019年从网上购买 $3$ 张电影票的费用比现场购买 $2$ 张电影票的费用少 $10$ 元:从网上购买 $5$ 张电影票的费用和现场购买 $1$ 张电影票的费用共 $200$ 元.

(1)、求该电影城2019年在网上购票和现场购票每张电影票的价格为多少元?

(2)、2019年五一当天，该电影城按照2019年网上购票和现场购票的价格销售电影票，当天售出的总票数为 $500$ 张.五一假期过后，观影人数出现下降，于是电影城决定从5月5日开始调整票价：现场购票价格下调，网上购票价格不变，结果发现，现场购票每张电影票的价格每降低 $2$ 元，售出总票数就比五一当天增加 $4$ 张.经统计，5月5日售出的总票数中有 $60 %$ 的电影票通过网上售出，其余通过现场售出，且当天票房总收入为 $17680$ 元，试求出5月5日当天现场购票每张电影票的价格为多少元?

查看试题解析
22. 如图1，平面直角坐标系中，B、C两点的坐标分别为B（0，3）和C（0，﹣ $\frac{9}{2}$ ），点A在x轴正半轴上，且满足∠BAO＝30°.

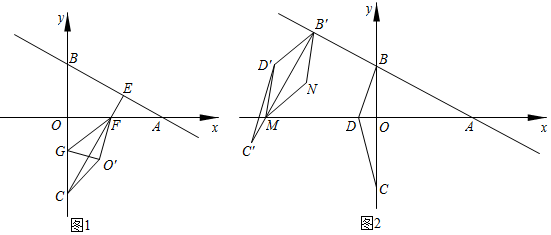(1)、过点C作CE⊥AB于点E，交AO于点F，点G为线段OC上一动点，连接GF，将△OFG沿FG翻折使点O落在平面内的点O′处，连接O′C，求线段OF的长以及线段O′C的最小值；

(2)、如图2，点D的坐标为D（﹣1，0），将△BDC绕点B顺时针旋转，使得BC⊥AB于点B，将旋转后的△BDC沿直线AB平移，平移中的△BDC记为△B′D′C′，设直线B′C′与x轴交于点M，N为平面内任意一点，当以B′、D′、M、N为顶点的四边形是菱形时，求点M的坐标.

查看试题解析