贵州省遵义市2020届九年级上学期数学10月月考试卷
试卷更新日期:2019-12-05 类型:月考试卷
一、单选题
-
1. 下列方程中,是一元二次方程的是( )A、x2+3x+y=0 B、x2+ +5=0 C、 D、x+y+1=02. 函数y=ax2(a≠0)的图象经过点(a,8),则a的值为( )
A、±2 B、-2 C、2 D、33. 已知关于x的一元二次方程 的一个根是0,则a的值为( )A、1 B、-1 C、1或-1 D、4. 二次函数 的最小值是 ( )A、 2 B、2 C、 1 D、15. 一元二次方程x2﹣x+2=0的根的情况是( )A、有两个相等的实数根 B、有两个不相等的实数根 C、无实数根 D、只有一个实数根6. 抛物线 向左平移3个单位,再向下平移2个单位后,所得的抛物线表达式是( )A、 B、 C、 D、7. 在一幅长 ,宽 的矩形风景画的四周镶一条金色纸边,制成一幅矩形挂图,如图所示,如果要使整幅挂图的面积是 ,设金色纸边的宽为 ,那么 满足的方程是( ) A、 B、 C、 D、8. 已知一个三角形的两边长是方程x2﹣8x+15=0的两根,则第三边y的取值范围是( )A、y<8 B、3<y<5 C、2<y<8 D、无法确定9. 不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )A、在y=x直线上 B、在直线y=-x上 C、在x轴上 D、在y轴上10. 已知 ,则 等于( )A、 或 B、6或1 C、 或1 D、2或311. 如图,正方形 边长为4个单位,两动点 、 分别从点 、 处,以1单位/ 、2单位/ 的速度逆时针沿边移动.记移动的时间为 , 面积为 (平方单位),当点 移动一周又回到点 终止,同时 点也停止运动,则 与 的函数关系图象为( )
A、 B、 C、 D、8. 已知一个三角形的两边长是方程x2﹣8x+15=0的两根,则第三边y的取值范围是( )A、y<8 B、3<y<5 C、2<y<8 D、无法确定9. 不论m取任何实数,抛物线y=a(x+m)2+m(a≠0)的顶点都( )A、在y=x直线上 B、在直线y=-x上 C、在x轴上 D、在y轴上10. 已知 ,则 等于( )A、 或 B、6或1 C、 或1 D、2或311. 如图,正方形 边长为4个单位,两动点 、 分别从点 、 处,以1单位/ 、2单位/ 的速度逆时针沿边移动.记移动的时间为 , 面积为 (平方单位),当点 移动一周又回到点 终止,同时 点也停止运动,则 与 的函数关系图象为( )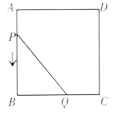 A、
A、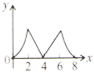 B、
B、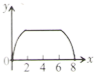 C、
C、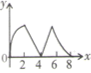 D、
D、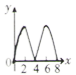
二、填空题
-
12. 把方程 化为一般形式为.13. 已知 , , 三点都在二次函数 的函数图象上,则 , , 的大小关系为.14. 若 , 是方程 的两根,则 .15. 如图, 中, , , ,分别以 、 、 为边作正方形 、 、 ,再作 ,使 ,点 在边 上,点 、 在边 上,点 、 在边 上,则 的长为.

三、解答题
-
16. 解方程:(1)、(2)、 ;17. 在实数范围内定义一种新运算“△”,其规则为:a△b=a2﹣b2 , 根据这个规则:(1)、求4△3的值;(2)、求(x+2)△5=0中x的值.18. 已知二次函数 的图象如图所示,求 的面积.
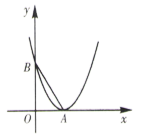 19. 关于x的一元二次方程 有实数根.(1)、求k的取值范围;(2)、若k是该方程的一个根,求 的值.20. 雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)、如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)、按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?21. 如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.
19. 关于x的一元二次方程 有实数根.(1)、求k的取值范围;(2)、若k是该方程的一个根,求 的值.20. 雅安地震牵动着全国人民的心,某单位开展了“一方有难,八方支援”赈灾捐款活动.第一天收到捐款10 000元,第三天收到捐款12 100元.(1)、如果第二天、第三天收到捐款的增长率相同,求捐款增长率;(2)、按照(1)中收到捐款的增长速度,第四天该单位能收到多少捐款?21. 如图,P是正方形ABCD对角线AC上一点,点E在BC上,且PE=PB.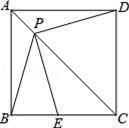 (1)、求证:PE=PD;(2)、连接DE,试判断∠PED的度数,并证明你的结论.22. 已知关于x的一元二次方程x2−(3k+1)x+2k2+2k=0.(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰△ABC的一边长a=6,另两边长b、c恰好分别是这个方程的两个根,求k的值.23. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
(1)、求证:PE=PD;(2)、连接DE,试判断∠PED的度数,并证明你的结论.22. 已知关于x的一元二次方程x2−(3k+1)x+2k2+2k=0.(1)、求证:无论k取何实数值,方程总有实数根;(2)、若等腰△ABC的一边长a=6,另两边长b、c恰好分别是这个方程的两个根,求k的值.23. 如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.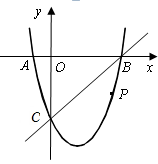 (1)、求二次函数解析式;(2)、连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
(1)、求二次函数解析式;(2)、连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.