2017年辽宁省锦州市高考数学一模试卷（理科）

试卷更新日期：2017-07-22 类型：高考模拟

进入出卷网下载

一、选择题：

1. 集合M={x|x=3ⁿ ， n∈N}，集合N={x|x=3n，n∈N}，则集合M与集合N的关系（）

A、M⊆N B、N⊆M C、M∩N=∅ D、M⊈N且N⊈M

查看试题解析
2. 若复数z满足i•z= $\frac{1}{2}$ （1+i），则z的虚部是（）

A、﹣ $\frac{1}{2}$ i B、 $\frac{1}{2}$ i C、﹣ $\frac{1}{2}$ D、 $\frac{1}{2}$

查看试题解析
3. 一个几何体的三视图如图所示，其中正视图和侧视图是腰长为2的两个全等的等腰直角三角形，俯视图是圆心角为 $\frac{π}{2}$ 的扇形，则该几何体的侧面积为（）

A、2 B、4+π C、4+ $\sqrt{2}$ π D、4+π+ $\sqrt{2}$ π

查看试题解析
4. 如表提供了某厂节能降耗改造后在生产A产品过程中记录的产量x（吨）与相应的生产能耗y（吨）的几组对应数据，根据表中提供的数据，求出y关于x的线性回归方程为 $\hat{y}$ =0.7x+0.35，则下列结论错误的是（）
x
3
4
5
6
y
2.5
t
4
4.5

A、线性回归直线一定过点（4.5，3.5） B、产品的生产能耗与产量呈正相关 C、t的取值必定是3.15 D、A产品每多生产1吨，则相应的生产能耗约增加0.7吨

查看试题解析
5. 已知等差数列{a_n}的前n项和S_n ，其中 $a_{1} + a_{5} = \frac{1}{2} S_{5}$ 且a₁₁=20，则S₁₃=（）

A、60 B、130 C、160 D、260

查看试题解析
6. 设p：实数x，y满足（x﹣1）²+（y﹣1）²≤2，q：实数x，y满足 ${\begin{matrix} y \geq x - 1 \\ y \geq 1 - x \\ y \leq 1 \end{matrix}$ ，则p是q的（）

A、必要不充分条件 B、充分不必要条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
7. 阅读下边的程序框图，运行相应的程序，输出的结果为（）

A、﹣2 B、 $\frac{1}{2}$ C、﹣1 D、2

查看试题解析
8. 三国时代吴国数学家赵爽所注《周髀算经》中给出了勾股定理的绝妙证明，下面是赵爽的弦图及注文，弦图是一个以勾股形之弦为边的正方形，其面积称为弦实，图中包含四个全等的勾股形及一个小正方形，分别涂成红（朱）色及黄色，其面积称为朱实，黄实，利用2×勾×股+（股﹣勾）²=4×朱实+黄实=弦实，化简，得勾²+股²=弦² ，设勾股中勾股比为1： $\sqrt{3}$ ，若向弦图内随机抛掷1000颗图钉（大小忽略不计），则落在黄色图形内的图钉数大约为（）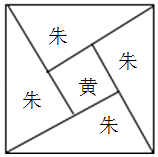

A、866 B、500 C、300 D、134

查看试题解析
9. 已知f（x）= $\sqrt{3}$ sinxcosx﹣sin²x，把f（x）的图象向右平移 $\frac{π}{12}$ 个单位，再向上平移2个单位，得到y=g（x）的图象，若对任意实数x，都有g（α﹣x）=g（α+x）成立，则g（α+ $\frac{π}{4}$ ）+g（ $\frac{π}{4}$ ）=（）

A、4 B、3 C、2 D、 $\frac{3}{2}$

查看试题解析
10. 设a＞0，b＞2，且a+b=3，则 $\frac{2}{a} + \frac{1}{b - 2}$ 的最小值是（）

A、6 B、 $2 \sqrt{2}$ C、 $4 \sqrt{2}$ D、 $3 + 2 \sqrt{2}$

查看试题解析
11. 已知双曲线 $\frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}}$ =1（a＞0，b＞0）左右焦点分别为F₁ ， F₂ ，渐近线为l₁ ， l₂ ， P位于l₁在第一象限内的部分，若l₂⊥PF₁ ， l₂∥PF₂ ，则双曲线的离心率为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{5}$ D、 $\sqrt{2}$

查看试题解析
12. 设函数f（x）在R上存在导数f′（x），∀x∈R，有f（﹣x）+f（x）=x² ，在（0，+∞）上f′（x）＜x，若f（2﹣m）+f（﹣m）﹣m²+2m﹣2≥0，则实数m的取值范围为（）

A、[﹣1，1] B、[1，+∞） C、[2，+∞） D、（﹣∞，﹣2]∪[2，+∞）

查看试题解析

二、填空题

13. （x²﹣x﹣2）³展开式中x项的系数为．

查看试题解析
14. 设抛物线x²=2y的焦点为F，经过点P（1，3）的直线l与抛物线相交于A，B两点，且点P恰为AB的中点，则 $| \vec{A F} | + | \vec{B F} |$ = ．

查看试题解析
15. 三棱锥S﹣ABC的所有顶点都在球O的球面上，△ABC是边长为3的正三角形，SC是球O的直径，且SC=4，则此三棱锥的体积V= ．

查看试题解析
16. 将正整数12分解成两个正整数的乘积有1×12，2×6，3×4三种，其中3×4是这三种分解中两数差的绝对值最小的，我们称3×4为12的最佳分解．当p×q（p≤q且pq∈N^* ，）是正整数n的最佳分解时，我们定义函数f（n）=q﹣p，例如f（12）=4﹣3=1．数列{f（3ⁿ）}的前100项和为．

查看试题解析

三、解答题

17. 已知函数 $f (x) = M s i n (ω x + φ) (M > 0 ， | φ | < \frac{π}{2})$ 的部分图象如图所示．

(1)、求函数f（x）的解析式；

(2)、在△ABC中，角A，B，C的对边分别是a，b，c，若（2a﹣c）cosB=bcosC，求 $f (\frac{A}{2})$ 的取值范围．

查看试题解析
18. 《汉字听写大会》不断创收视新高，为了避免“书写危机”弘扬传统文化，某市对全市10万名市民进行了汉字听写测试，调查数据显示市民的成绩服从正态分布N（168，16）．现从某社区居民中随机抽取50名市民进行听写测试，发现被测试市民正确书写汉字的个数全部在160到184之间，将测试结果按如下方式分成六组：第一组[160，164），第二组[164，168），…，第六组[180，184），如图是按上述分组方法得到的频率分布直方图．

(1)、试评估该社区被测试的50名市民的成绩在全市市民中成绩的平均状况及这50名市民成绩在172个以上（含172个）的人数；

(2)、在这50名市民中成绩在172个以上（含172个）的人中任意抽取2人，该2人中成绩排名（从高到低）在全市前130名的人数记为ξ，求ξ的数学期望．
参考数据：若η～N（μ，σ²），则P（μ﹣σ＜X＜μ+σ）=0.6826，P（μ﹣2σ＜X＜μ+2σ）=0.9544，P（μ﹣3σ＜X＜μ+3σ）=0.9974．

查看试题解析
19. 在四棱锥P﹣ABCD中， $∠ D B A = \frac{π}{2}$ ， $A B \underline{\underline{∥}} C D$ ，△PAB和△PBD都是边长为2的等边三角形，设P在底面ABCD的射影为O．

(1)、求证：O是AD中点；

(2)、证明：BC⊥PB；

(3)、求二面角A﹣PB﹣C的余弦值．

查看试题解析
20. 已知椭圆C： $\frac{y^{2}}{a^{2}}$ + $\frac{x^{2}}{b^{2}}$ =1（a＞b＞0）的上下两个焦点分别为F₁ ， F₂ ，过点F₁与y轴垂直的直线交椭圆C于M，N两点，△MNF₂的面积为 $\sqrt{3}$ ，椭圆C的离心率为 $\frac{\sqrt{3}}{2}$
（Ⅰ）求椭圆C的标准方程；
（Ⅱ）已知O为坐标原点，直线l：y=kx+m与y轴交于点P，与椭圆C交于A，B两个不同的点，若存在实数λ，使得 $\vec{O A}$ +λ $\vec{O B}$ =4 $\vec{O P}$ ，求m的取值范围．

查看试题解析
21. 已知m＞0，设函数f（x）=e^mx﹣lnx﹣2．

(1)、若m=1，证明：存在唯一实数 $t \in (\frac{1}{2} ， 1)$ ，使得f′（t）=0；

(2)、若当x＞0时，f（x）＞0，证明： $m > e^{- \frac{1}{2}}$ ．

查看试题解析
22. 已知曲线C在平面直角坐标系xOy下的参数方程为 ${\begin{matrix} x = 1 + \sqrt{3} c o s θ \\ y = \sqrt{3} s i n θ \end{matrix}$ （θ为参数），以坐标原点O为极点，以x轴正半轴为极轴，建立极坐标系．

(1)、求曲线C的普通方程及极坐标方程；

(2)、直线l的极坐标方程是 $ρ c o s (θ - \frac{π}{6}) = 3 \sqrt{3}$ ，射线OT： $θ = \frac{π}{3} (ρ > 0)$ 与曲线C交于点A与直线l交于点B，求线段AB的长．

查看试题解析
23. 已知函数f（x）=|x+3|+|x﹣2|
（Ⅰ）若∀x∈R，f（x）≥6a﹣a²恒成立，求实数a的取值范围
（Ⅱ）求函数y=f（x）的图象与直线y=9围成的封闭图形的面积．

查看试题解析

x	3	4	5	6
y	2.5	t	4	4.5