2017年高考真题分类汇编（理数）：专题8 复数、算法、推理及选考部分

试卷更新日期：2017-07-21 类型：二轮复习

进入出卷网下载

一、单选题

1. 已知a∈R，i是虚数单位，若z=a+ $\sqrt{3}$ i，z• $\bar{z}$ =4，则a=（　　）

A、1或﹣1 B、 $\sqrt{7}$ 或﹣ $\sqrt{7}$ C、﹣ $\sqrt{3}$ D、 $\sqrt{3}$

查看试题解析
2.
阅读右面的程序框图，运行相应的程序，若输入N的值为24，则输出N的值为（　　）

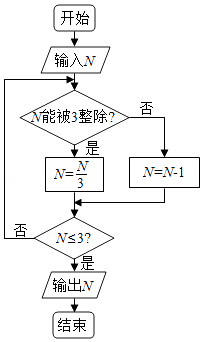A、0 B、1 C、2 D、3

查看试题解析
3.
执行如图所示的程序框图，输出的S值为（　　）

A、2 B、 $\frac{3}{2}$ C、 $\frac{5}{3}$ D、 $\frac{8}{5}$

查看试题解析
4. 若复数（1﹣i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是（　　）

A、（﹣∞，1） B、（﹣∞，﹣1） C、（1，+∞） D、（﹣1，+∞）

查看试题解析
5. $\frac{3 + i}{1 + i}$ =（）

A、1+2i B、1﹣2i C、2+i D、2﹣i

查看试题解析
6. 设复数z满足（1+i）z=2i，则|z|=（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析
7.
执行两次如图所示的程序框图，若第一次输入的x值为7，第二次输入的x值为9，则第一次，第二次输出的a值分别为（　　）

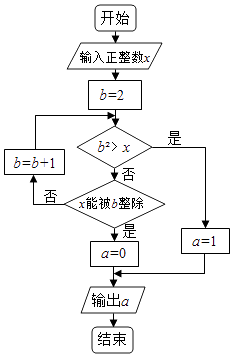A、0，0 B、1，1 C、0，1 D、1，0

查看试题解析
8. 设有下面四个命题
p₁：若复数z满足 $\frac{1}{z}$ ∈R，则z∈R；
p₂：若复数z满足z²∈R，则z∈R；
p₃：若复数z₁ ， z₂满足z₁z₂∈R，则z₁= $\bar{z_{2}}$ ；
p₄：若复数z∈R，则 $\bar{z}$ ∈R．
其中的真命题为（　　）

A、p₁ ， p₃ B、p₁ ， p₄ C、p₂ ， p₃ D、p₂ ， p₄

查看试题解析
9.
执行如图的程序框图，如果输入的a=﹣1，则输出的S=（）

A、2 B、3 C、4 D、5

查看试题解析
10. 甲、乙、丙、丁四位同学一起去问老师询问成语竞赛的成绩．老师说：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩．看后甲对大家说：我还是不知道我的成绩．根据以上信息，则（）

A、乙可以知道四人的成绩 B、丁可以知道四人的成绩 C、乙、丁可以知道对方的成绩 D、乙、丁可以知道自己的成绩

查看试题解析
11.
执行如图的程序框图，为使输出S的值小于91，则输入的正整数N的最小值为（）

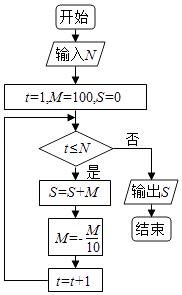A、5 B、4 C、3 D、2

查看试题解析

二、填空题

12. 已知复数z=（1+i）（1+2i），其中i是虚数单位，则z的模是．

查看试题解析
13.
如图是一个算法流程图：若输入x的值为 $\frac{1}{16}$ ，则输出y的值是．

查看试题解析
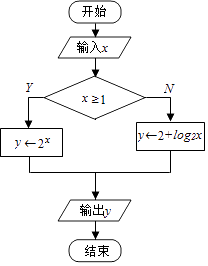14. 在极坐标系中，点A在圆ρ²﹣2ρcosθ﹣4ρsinθ+4=0上，点P的坐标为（1，0），则|AP|的最小值为．

查看试题解析
15. 已知a、b∈R，（a+bi）²=3+4i（i是虚数单位），则a²+b²= ， ab= ．

查看试题解析
16. 已知a∈R，i为虚数单位，若 $\frac{a - i}{2 + i}$ 为实数，则a的值为．

查看试题解析
17. 在极坐标系中，直线4ρcos（θ﹣ $\frac{π}{6}$ ）+1=0与圆ρ=2sinθ的公共点的个数为．

查看试题解析

三、选考部分

18. 在直角坐标系xOy中，直线l₁的参数方程为 ${\begin{matrix} x = 2 + t \\ y = k t \end{matrix}$ ，（t为参数），直线l₂的参数方程为 ${\begin{matrix} x = - 2 + m \\ y = \frac{m}{k} \end{matrix}$ ，（m为参数）．设l₁与l₂的交点为P，当k变化时，P的轨迹为曲线C．

（Ⅰ）写出C的普通方程；

（Ⅱ）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l₃：ρ（cosθ+sinθ）﹣ $\sqrt{2}$ =0，M为l₃与C的交点，求M的极径．

查看试题解析
19. 已知函数f（x）=|x+1|﹣|x﹣2|．

（Ⅰ）求不等式f（x）≥1的解集；

（Ⅱ）若不等式f（x）≥x²﹣x+m的解集非空，求m的取值范围．

查看试题解析
20. 在直角坐标系xOy中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C₁的极坐标方程为ρcosθ=4．

（Ⅰ）M为曲线C₁上的动点，点P在线段OM上，且满足|OM|•|OP|=16，求点P的轨迹C₂的直角坐标方程；

（Ⅱ）设点A的极坐标为（2， $\frac{π}{3}$ ），点B在曲线C₂上，求△OAB面积的最大值．

查看试题解析
21. 已知a＞0，b＞0，a³+b³=2，证明：

（Ⅰ）（a+b）（a⁵+b⁵）≥4；

（Ⅱ）a+b≤2．

查看试题解析
22. [选修4-4 ，坐标系与参数方程]
在直角坐标系xOy中，曲线C的参数方程为 ${\begin{matrix} x = 3 c o s θ \\ y = s i n θ \end{matrix}$ （θ为参数），直线l的参数方程为 ${\begin{matrix} x = a + 4 t \\ y = 1 - t \end{matrix}$ （t为参数）．

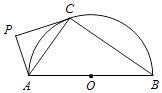
(1)、若a=﹣1，求C与l的交点坐标；

(2)、若C上的点到l距离的最大值为 $\sqrt{17}$ ，求a．

查看试题解析
23. 已知函数f（x）=﹣x²+ax+4，g（x）=|x+1|+|x﹣1|．

(1)、当a=1时，求不等式f（x）≥g（x）的解集；

(2)、若不等式f（x）≥g（x）的解集包含[﹣1，1]，求a的取值范围．

查看试题解析
24.
如图，AB为半圆O的直径，直线PC切半圆O于点C，AP⊥PC，P为垂足．
求证：（Ⅰ）∠PAC=∠CAB；
（Ⅱ）AC²=AP•AB．

查看试题解析
25. 已知矩阵A= $[\begin{matrix} 0 & 1 \\ 1 & 0 \end{matrix}]$ ，B= $[\begin{matrix} 1 & 0 \\ 0 & 2 \end{matrix}]$ ．
（Ⅰ）求AB；
（Ⅱ）若曲线C₁： $\frac{x^{2}}{8} + \frac{y^{2}}{2}$ =1在矩阵AB对应的变换作用下得到另一曲线C₂ ，求C₂的方程．

查看试题解析
26. 在平面直角坐标系xOy中，已知直线l的参数方程为 ${\begin{matrix} x = - 8 + t \\ y = \frac{t}{2} \end{matrix}$ （t为参数），曲线C的参数方程为 ${\begin{matrix} x = 2 s^{2} \\ y = 2 \sqrt{2} s \end{matrix}$ （s为参数）．设P为曲线C上的动点，求点P到直线l的距离的最小值．

查看试题解析
27. 已知a，b，c，d为实数，且a²+b²=4，c²+d²=16，证明ac+bd≤8．

查看试题解析